基礎322

R5.07-1B2

R5.01-1B2

R4.07-2A7

R2.11-2A7

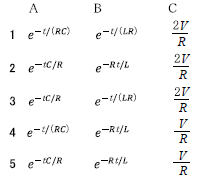
R3.07-1B2

H31.01-1B2

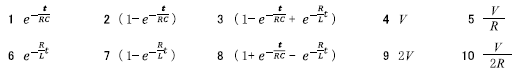
解答

R5.07-1B2

ア　6：\(e^{-\frac{t}{RC}}\)
イ　7：\((1-e^{-\frac{R}{L}t})\)
ウ　3：\((1+e^{-\frac{t}{RC}}-e^{-\frac{R}{L}t})\)
エ　9：V
オ　5：\(\frac{V}{R}\)

ワンポイント解説
　過渡現象RL,RC

R5.01-1B2

ア　1：0
イ　2：\(\frac{V}{R}\)
ウ　8：\((1-ε^{-Rt/L})\)
エ　9：\((1-\frac{1}{ε})\)
オ　10：時定数

ワンポイント解説
　過渡現象RL

R4.07-2A7

\(２　e^{-t/(RC)}　　　e^{-Rt/L}　　　\frac{V}{R}\)

ワンポイント解説
　過渡現象RL,RC

R2.11-2A7

\(４　e^{-t/(RC)}　　　e^{-Rt/L}　　　\frac{V}{R}\)

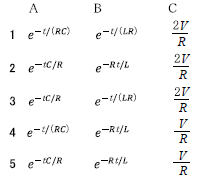
R3.07-1B2

ア　6：\(e^{-\frac{t}{RC}}\)
イ　2：\((1-e^{-\frac{R}{L}t})\)
ウ　3：\((1+e^{-\frac{t}{RC}}-e^{-\frac{R}{L}t})\)
エ　9：\(V\)
オ　10：\(\frac{V}{R}\)

ワンポイント解説
　過渡現象RL,RC

H31.01-1B2

ア　1：\(e^{-\frac{t}{RC}}\)
イ　7：\((1-e^{-\frac{R}{L}t})\)
ウ　8：\((1+e^{-\frac{t}{RC}}-e^{-\frac{R}{L}t})\)
エ　4：\(V\)
オ　5：\(\frac{V}{R}\)

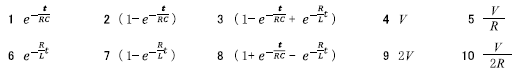
検索用キーワード（問題文の最初の一文）

図に示す回路の過渡現象
図に示す抵抗R[Ω]と自己インダクタンスL[H]を直列に接続した回路の過渡現象