R5.01-2B5
R3.07-1B5
解答
R5.01-2B5
ア 5:1
イ 9:2
ウ 8:\(\frac{1}{2}\)
エ 2:\(I_1\)
オ 6:45

ワンポイント解説
オームの法則をガンガン使い、\(I_1,I_2,I_0\)などを先ず求める。
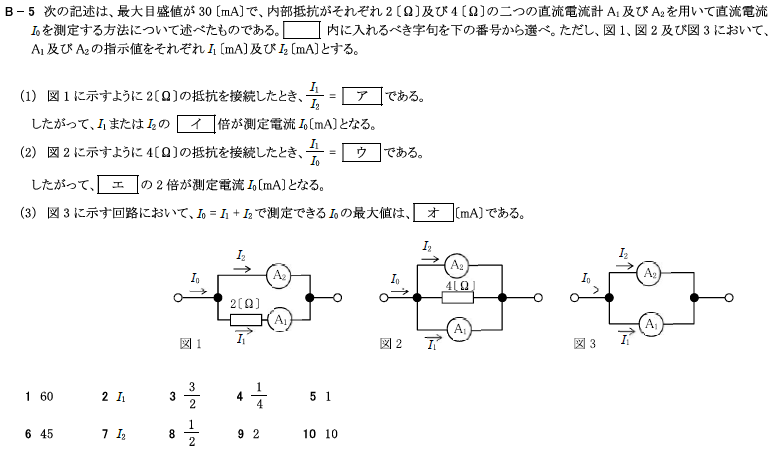
(1) 図1に示すように2[Ω]の抵抗を接続したとき、
両端子(〇)間の電圧Vとすると、
\(I_1=\frac{V}{R}=\frac{V}{2+2}=\frac{V}{4}\)
\(I_2=\frac{V}{4}\)
\(V=4I_1=4I_2\)より、
\(\frac{I_1}{I_2}\)=1 ーア
したがって、アより、
\(I_0=I_1+I_2=2I_1=2I_2\)になるので、
\(I_1\)または\(I_2\)の2倍が測定電流\(I_0\)[mA]となる。 -イ
(2) 図2に示すように4[Ω]の抵抗を接続したとき、
両端子(〇)間の電圧Vとすると、
\(I_1=\frac{V}{R}=\frac{V}{2}\)
\(I_2=\frac{V}{4}\)
4[Ω]の抵抗に流れる電流を\(I_R\)とすると、
\(I_R=\frac{V}{4}\)
\(I_0=I_1+I_2+I_R=\frac{V}{2}+\frac{V}{4}+\frac{V}{4}=V\)
\(\frac{I_1}{I_0}=\frac{\frac{V}{2}}{V}=\frac{1}{2}\) ーウ
したがって、ウより、
\(I_0=2I_1\)になるので、
\(I_1\)の2倍が測定電流\(I_0\)[mA]となる。 -エ
(3) 図3に示す回路において、\(I_0=I_1+I_2\)で測定できる\(I_0\)の最大値は、
ワンポイント解説
各電流計の電圧を求めて、最小の電圧を考慮する。
(それ以上だと電流計が壊れてしまうため)
\(V_1=R×I=2×30m=60m [V]\)
\(V_2=4×30m=120m [V]\)
よって、\(V_1=60m [V]\)となるように設計する。
\(I_1=\frac{V}{R}=\frac{60m}{2}=30m [A]\)
\(I_2=\frac{60m}{4}=15m [A]\)
\(I_0=I_1+I_2=30m+15m=45m [A]\) -オ
R3.07-1B5
ア 10:1
イ 9:2
ウ 3:\(\frac{1}{2}\)
エ 2:\(I_1\)
オ 1:15

ア~エは上の問題と同じ。
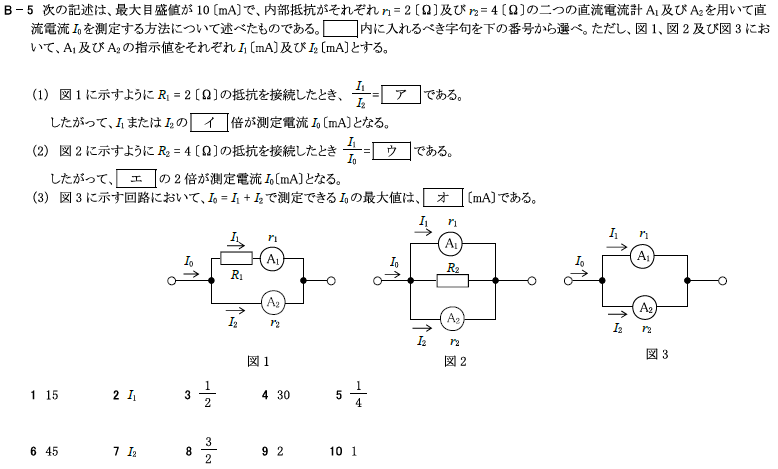
(3) 図3に示す回路において、\(I_0=I_1+I_2\)で測定できる\(I_0\)の最大値は、
ワンポイント解説
各電流計の電圧を求めて、最小の電圧を考慮する。
(それ以上だと電流計が壊れてしまうため)
\(V_1=R×I=2×10m=20m [V]\)
\(V_2=4×10m=40m [V]\)
よって、\(V_1=20m [V]\)となるように設計する。
\(I_1=\frac{V}{R}=\frac{20m}{2}=10m [A]\)
\(I_2=\frac{20m}{4}=5m [A]\)
\(I_0=I_1+I_2=10m+5m=15m [A]\) -オ
検索用キーワード(問題文の最初の一文)
最大目盛値が\(30\)[mA]で、内部抵抗がそれぞれ\(2\)[Ω]及び\(4\)[Ω]の二つの直流電流計\(A_1\)及び\(A_2\)を用いて直流電流\(I_0\)を測定する方法
最大目盛値が\(10\)[mA]で、内部抵抗がそれぞれ\(r_1=2\)[Ω]及び\(r_2=4\)[Ω]の二つの直流電流計\(A_1\)及び\(A_2\)を用いて直流電流\(I_0\)を測定する方法


コメント