R5.01-2A4
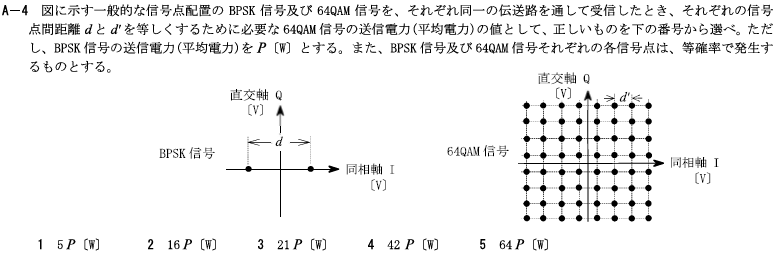
R3.07-2A6
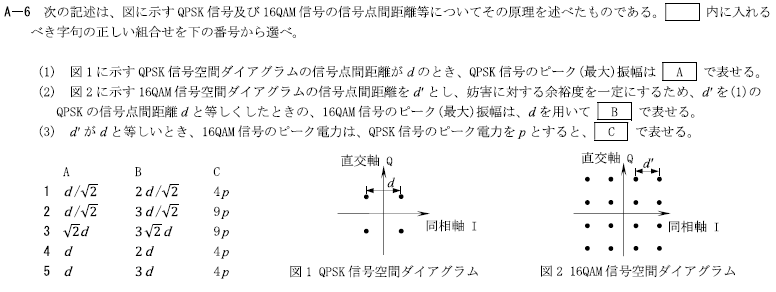
R3.01-1A2
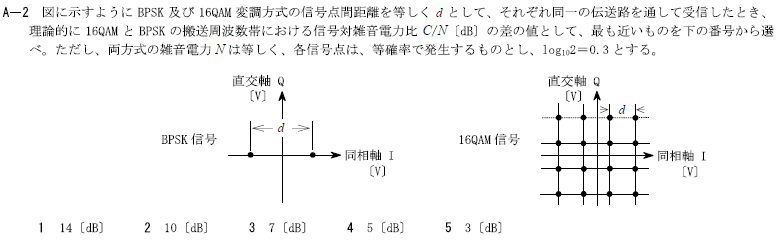
R1.07-1A3
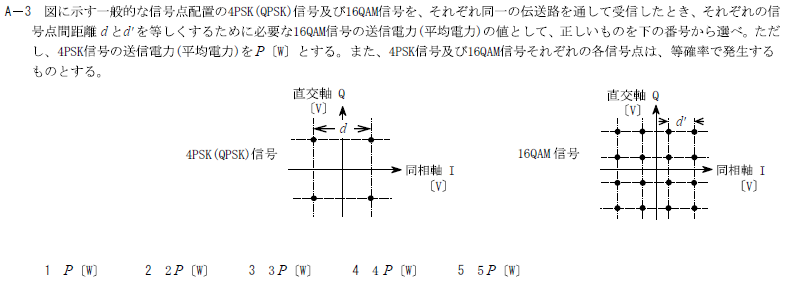
H31.01-1A3
解答
R5.01-2A4
4 42P[W]
ワンポイント解説
最大電力または、平均電力で求め方が異なります。

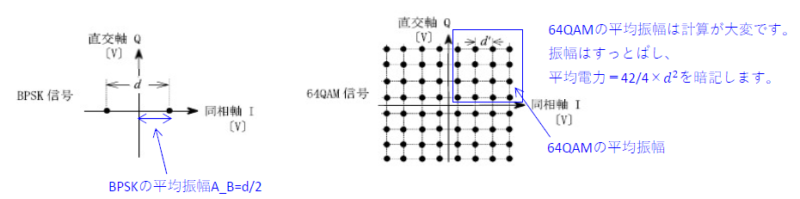
■平均電力
(1)BPSKの平均振幅\(A_B=\frac{d}{2}\)
(2)64QAMの各振幅は計算をせずに暗記します。下記※参照。
(3)BPSKの平均電力\(P_B\)(=Pとする)は、
\(P_B=A_B^2=(\frac{d}{2})^2=\frac{d^2}{4}=P\)
64QAMの平均電力\(P_{64}\)は、各振幅の二乗平均をとって
\(P_{64}=\frac{42}{4}d^2\) -※
したがって、
\(\frac{P_{64}}{P_B}=\frac{\frac{42}{4}d^2}{\frac{d^2}{4}}\)
\(=42P\)
ワンポイント解説
各平均電力
64QAMの平均電力\(P_{64}=\frac{42}{4}d^2\)
16QAMの平均電力\(P_{16}=\frac{10}{4}d^2\)
R3.07-2A6
2 \(d/\sqrt{2} 3d/\sqrt{2} 9p\)
■最大電力
(1)QPSKの最大振幅\(A_Q\)
(2)16QAMの最大振幅\(A_{16}\)
(3)QPSKの電力\(P_Q\)(=Pとする)と16QAMの電力\(P_{16}\)の比は、
\(\frac{P_{16}}{P_Q}=\frac{A_{16}^2}{A_Q^2}\)


■最大電力
(1)QPSKの最大振幅\(A_Q=\sqrt{(\frac{d}{2})^2+(\frac{d}{2})^2}=\sqrt{\frac{2d^2}{4}}=\frac{d}{\sqrt{2}}\)
(2)16QAMの最大振幅\(A_{16}=\sqrt{(\frac{3d}{2})^2+(\frac{3d}{2})^2}=\sqrt{\frac{18d^2}{4}}=\frac{3d}{\sqrt{2}}\)
(3)QPSKの電力\(P_Q\)(=Pとする)と16QAMの電力\(P_{16}\)の比は、
\(\frac{P_{16}}{P_Q}=\frac{A_{16}^2}{A_Q^2}=\frac{(\frac{3d}{\sqrt{2}})^2}{(\frac{d}{\sqrt{2}})^2}=\frac{\frac{9d^2}{2}}{\frac{d^2}{2}}=9P\)
R3.01-1A2
2 10[dB]

■平均電力
(1)BPSKの平均振幅\(A_B=\frac{d}{2}\)
(2)16QAMの各振幅
一つ目:\(A_{16①}=\frac{\sqrt{2}d}{2}\)
二つ目:\(A_{16②}=\sqrt{(\frac{3}{2}d)^2+(\frac{1}{2}d)^2}=\sqrt{\frac{10}{2^2}d^2}=\frac{\sqrt{10}d}{2}\)
三つ目:\(A_{16③}=\sqrt{(\frac{1}{2}d)^2+(\frac{3}{2}d)^2}=\sqrt{\frac{10}{2^2}d^2}=\frac{\sqrt{10}d}{2}\)
四つ目:\(A_{16④}=\frac{3\sqrt{2}d}{2}\)
(3)BPSKの平均電力\(P_B\)(=Pとする)は、
\(P_B=A_B^2=(\frac{d}{2})^2=\frac{d^2}{4}=P\)
16QAMの平均電力\(P_{16}\)は、各振幅の二乗平均をとって
\(P_{16}=\frac{1}{4}×\{(A_{16①})^2+(A_{16②})^2+(A_{16③})^2+(A_{16④})^2\}\)
\(=\frac{1}{4}×\{(\frac{\sqrt{2}d}{2})^2+(\frac{\sqrt{10}d}{2})^2+(\frac{\sqrt{10}d}{2})^2+(\frac{3\sqrt{2}d}{2})^2\}\)
\(=\frac{1}{4}×(\frac{d^2}{2}+\frac{5d^2}{2}+\frac{5d^2}{2}+\frac{9d^2}{2})\)
\(=\frac{1}{4}×\frac{20}{2}d^2\)
したがって、
\(\frac{P_{16}}{P_B}=\frac{\frac{1}{4}×\frac{20}{2}d^2}{\frac{d^2}{4}}\)
\(=10P\)(真数)
デシベル計算より、
10(真数)=10[dB]
※平均電力は暗記しましょう。その方が早いです。
ワンポイント解説
各平均電力
64QAMの平均電力\(P_{64}=\frac{42}{4}d^2\)
16QAMの平均電力\(P_{16}=\frac{10}{4}d^2\)
R1.07-1A3
5 5P[W]

■平均電力
(1)4PSKの平均振幅\(A_4=\frac{\sqrt{2}d}{2}\)
(2)16QAMの各振幅
一つ目:\(A_{16①}=\frac{\sqrt{2}d}{2}\)
二つ目:\(A_{16②}=\sqrt{(\frac{3}{2}d)^2+(\frac{1}{2}d)^2}=\sqrt{\frac{10}{2^2}d^2}=\frac{\sqrt{10}d}{2}\)
三つ目:\(A_{16③}=\sqrt{(\frac{1}{2}d)^2+(\frac{3}{2}d)^2}=\sqrt{\frac{10}{2^2}d^2}=\frac{\sqrt{10}d}{2}\)
四つ目:\(A_{16④}=\frac{3\sqrt{2}d}{2}\)
(3)4PSKの平均電力\(P_4\)(=Pとする)は、
\(P_4=A_4^2=(\frac{\sqrt{2}d}{2})^2=\frac{d^2}{2}=P\)
16QAMの平均電力\(P_{16}\)は、各振幅の二乗平均をとって
\(P_{16}=\frac{1}{4}×\{(A_{16①})^2+(A_{16②})^2+(A_{16③})^2+(A_{16④})^2\}\)
\(=\frac{1}{4}×\{(\frac{\sqrt{2}d}{2})^2+(\frac{\sqrt{10}d}{2})^2+(\frac{\sqrt{10}d}{2})^2+(\frac{3\sqrt{2}d}{2})^2\}\)
\(=\frac{1}{4}×(\frac{d^2}{2}+\frac{5d^2}{2}+\frac{5d^2}{2}+\frac{9d^2}{2})\)
\(=\frac{1}{4}×\frac{20}{2}d^2\)
したがって、
\(\frac{P_{16}}{P_4}=\frac{\frac{1}{4}×\frac{20}{2}d^2}{\frac{d^2}{2}}\)
\(=5P\)(真数)
H31.01-1A3
1 \(d/\sqrt{2} 3d/\sqrt{2} 9p\)

■最大電力
(1)QPSKの最大振幅\(A_Q=\sqrt{(\frac{d}{2})^2+(\frac{d}{2})^2}=\sqrt{\frac{2d^2}{4}}=\frac{d}{\sqrt{2}}\)
(2)16QAMの最大振幅\(A_{16}=\sqrt{(\frac{3d}{2})^2+(\frac{3d}{2})^2}=\sqrt{\frac{18d^2}{4}}=\frac{3d}{\sqrt{2}}\)
(3)QPSKの電力\(P_Q\)(=Pとする)と16QAMの電力\(P_{16}\)の比は、
\(\frac{P_{16}}{P_Q}=\frac{A_{16}^2}{A_Q^2}=\frac{(\frac{3d}{\sqrt{2}})^2}{(\frac{d}{\sqrt{2}})^2}=\frac{\frac{9d^2}{2}}{\frac{d^2}{2}}=9P\)
検索用キーワード(問題文の最初の一文)
・図に示す一般的な信号点配置のBPSK信号及び64QAM信号を、それぞれ同一の伝送路を通して受信したとき、それぞれの信号点間距離dとd’を等しくするために必要な64QAM信号の送信電力(平均電力)の値
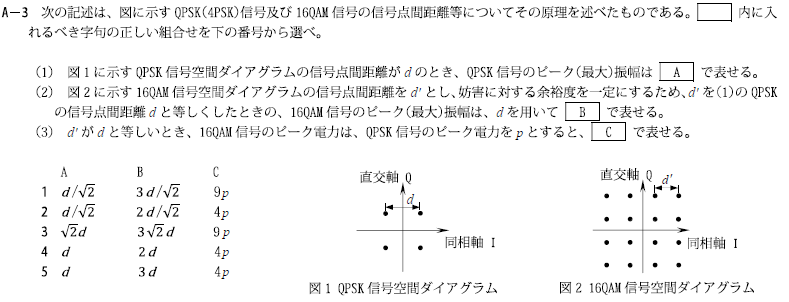
・図に示すQPSK信号及び16QAM信号の信号点間距離等についてその原理
・図に示すようにBPSK信号及び16QAM変調方式の信号点間距離を等しくdとして、それぞれ同一の伝送路を通して受信したとき、理論的に16QAMとBPSKの搬送周波数帯における信号対雑音電力比C/N[dB]の差の値
・図に示す一般的な信号点配置の4PSK(QPSK)信号及び16QAM信号を、それぞれ同一の伝送路を通して受信したとき、それぞれの信号点間距離dとd’を等しくするために必要な16QAM信号の送信電力(平均電力)の値
・図に示すQPSK(4PSK)信号及び16QAM信号の信号点間距離等についてその原理


コメント