R5.01-2A20

R2.11-1A19

R4.01-1A19

R2.11-2A19

解答
R5.01-2A20
5 \(21Z_o/20\)[Ω]
ワンポイント解説
π形抵抗減衰器の公式
\(R_1=\frac{(n^2-1)Z_O}{2n}\)
\(R_2=\frac{(n+1)Z_O}{n-1}\)
解き方
①減衰量[dB]から減衰量\(\frac{1}{n}\)を求める。
※ただし、抵抗減衰器のデシベル計算は電圧扱いです。
∵減衰量は電圧の減衰量だからです。
参考:\(\frac{1}{n}=\frac{R_2Z_O}{R_1R_2+R_2Z_O+Z_OR_1}\)
②公式にnを代入。

①減衰量[dB]から減衰量\(\frac{1}{n}\)を求める。
※ただし、抵抗減衰器のデシベル計算は電圧扱いです。
デシベル計算 ※電圧は2倍
+10dB=10倍 +3dB=2倍
-10dB=1/10倍 -3dB=1/2倍
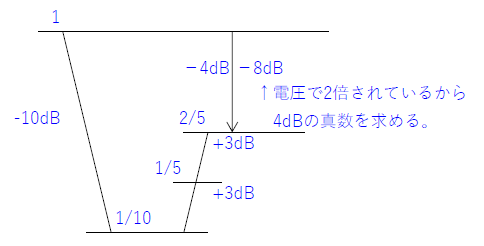
よって、減衰量\(8[dB]=\frac{2}{5}=\frac{1}{\frac{5}{2}}=\frac{1}{n}\)より、\(n=\frac{5}{2}\)
②公式にnを代入。
\(R_1=\frac{(n^2-1)Z_O}{2n}=\frac{(\frac{5}{2}^2-1)Z_O}{2×\frac{5}{2}}=\frac{(\frac{25-4}{4})Z_O}{5}=\frac{21Z_O}{20}\)
R2.11-1A19
1 \(3Z_o/2\)[Ω]

①減衰量[dB]から減衰量\(\frac{1}{n}\)を求める。
※ただし、抵抗減衰器のデシベル計算は電圧扱いです。
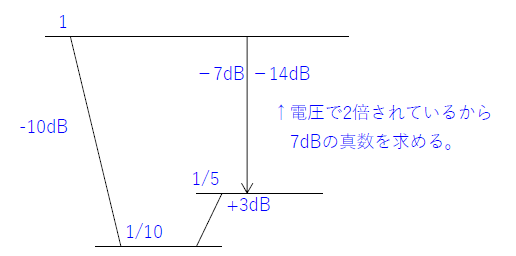
よって、減衰量\(14[dB]=\frac{1}{5}=\frac{1}{n}\)より、\(n=5\)
②公式にnを代入。
\(R_2=\frac{(n+1)Z_O}{n-1}=\frac{(5+1)Z_O}{5-1}=\frac{3Z_O}{2}\)
R4.01-1A19
5 \(5Z_o/12\)[Ω]
ワンポイント解説
T形抵抗減衰器の公式
\(R_1=\frac{(n-1)Z_O}{n+1}\)
\(R_2=\frac{2nZ_O}{n^2-1}\)
解き方
①減衰量[dB]から減衰量\(\frac{1}{n}\)を求める。
※ただし、抵抗減衰器のデシベル計算は電圧扱いです。
∵減衰量は電圧の減衰量だからです。
参考:\(\frac{1}{n}=\frac{R_2}{R_1+R_2+Z_O}\)
②公式にnを代入。

①減衰量[dB]から減衰量\(\frac{1}{n}\)を求める。
※ただし、抵抗減衰器のデシベル計算は電圧扱いです。

よって、減衰量\(14[dB]=\frac{1}{5}=\frac{1}{n}\)より、\(n=5\)
②公式にnを代入。
\(R_2=\frac{2nZ_O}{n^2-1}=\frac{2×5Z_O}{5^2-1}=\frac{10Z_O}{24}=\frac{5Z_O}{12}\)
R2.11-2A19
1 \(2Z_o/3\)[Ω]

①減衰量[dB]から減衰量\(\frac{1}{n}\)を求める。
※ただし、抵抗減衰器のデシベル計算は電圧扱いです。

よって、減衰量\(14[dB]=\frac{1}{5}=\frac{1}{n}\)より、\(n=5\)
②公式にnを代入。
\(R_1=\frac{(n-1)Z_O}{n+1}=\frac{(5-1)Z_O}{5+1}=\frac{(2)Z_O}{3}\)
公式を並べてみると以下になります。規則性がありますね。
片方をさえ覚えれば、上下を入れ替えれば、、、 省エネ出来ますね!
| π形 | T形 |
| \(R_1=\frac{n^2-1}{2n}Z_O\) | \(R_1=\frac{n-1}{n+1}Z_O\) |
| \(R_2=\frac{n+1}{n-1}Z_O\) | \(R_2=\frac{2n}{n^2-1}Z_O\) |
検索用キーワード(問題文の最初の一文)
・図の回路に示す抵抗素子\(R_1\)[Ω]及び\(R_2\)[Ω]で構成される抵抗減衰器において、減衰量を8[dB]にするための抵抗素子\(R_1\)の値を表す式
・減衰量を14[dB]にするための抵抗素子\(R_2\)の値を表す式


コメント