無線工学209(2)

R5.6b-4

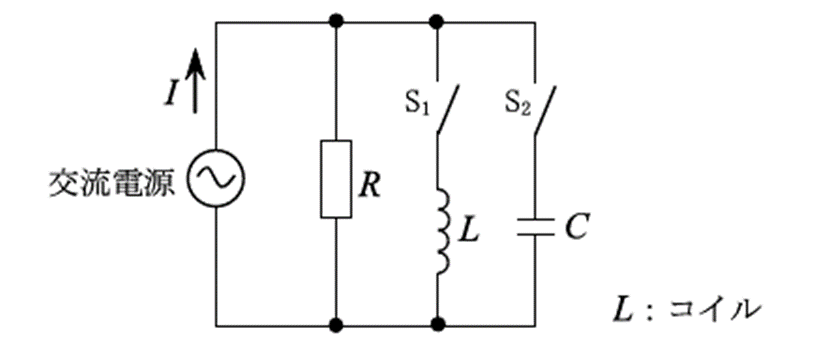
　図に示す回路において、スイッチ\(S_1\)のみを閉じたときの電流\(I\)とスイッチ\(S_2\)のみを閉じたときの電流Iは、ともに\(5〔A〕\)であった。また、スイッチ\(S_1\)と\(S_2\)の両方を閉じたときの電流\(I\)は、\(4〔A〕\)であった。抵抗\(R\)及びコイル\(L\)のリアクタンス\(X_L\)の値の組合せとして、正しいものを下の番号から選べ。ただし、交流電源電圧は\(96〔V〕\)とする。

　　\(R\)　　　　　　　 \(X_L\)

１　19.2 〔Ω〕　　　 10.7 〔Ω〕

２　19.2 〔Ω〕　　　 32.0 〔Ω〕

３　24.0 〔Ω〕　　　 10.7 〔Ω〕

４　24.0 〔Ω〕　　　 32.0 〔Ω〕

解答

４　24.0 〔Ω〕　　　 32.0 〔Ω〕

解き方

①\(S_1\)と\(S_2\)の両方を閉じたときの全電流を\(I_{12}\)とすると、
　抵抗\(R=\frac{E}{I_{12}}=\frac{96}{4}=24.0　[Ω]\)

②割合\(5:4:3\)で\(X_L\)、\(X_C\)を求める
　1.スイッチ片方閉じた電流を斜面に書く
　2.スイッチ両方閉じた電流を底面に書く
　3.割合\(5:4:3\)で残りの数字を縦に書く

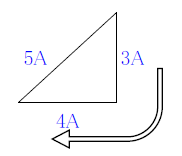
　4.矢印の方向の分数をＲにかける。
　　この場合は、\(\frac{4}{3}\)
2.求める\(X_L\)は\(R\)と②の4で求めた数字を掛け合わせる
　\(X_L=R×\frac{4}{3}=24.0×\frac{4}{3}=32　[Ω]\)