無線工学202(3)

R5.6a-3（R5.6b-3）

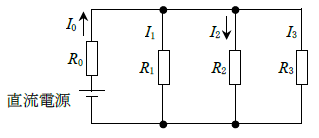
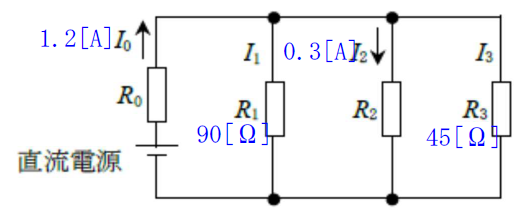
　図に示す回路において、抵抗\(R_0\)〔Ω〕に流れる電流\(I_0\)が1.2〔A〕、抵抗\(R_2\)に流れる電流\(I_2\)が0.3〔A〕であった。このとき\(R_2\)の値として、正しいものを下の番号から選べ。ただし、抵抗\(R_1\)及び\(R_3\)をそれぞれ90〔Ω〕及び45〔Ω〕とする。

１　20〔Ω〕

２　40〔Ω〕

３　60〔Ω〕

４　90〔Ω〕

５　120〔Ω〕

解答

４　90〔Ω〕

解き方
①\(I_1\)または、\(I_3\)を求める。
　\(I_0=I_1+I_2+I_3\)　だから、
　\(1.2=I_1+0.3+I_3\)
　\(I_1+I_3=0.9\)

②\(R_1\)と\(R_3\)の抵抗から電流\(I_1\)、\(I_3\)を求める。
　\(R_1(90Ω)\)と\(R_3(45Ω)\)は2：1なので
　電流は抵抗値に応じて流れるから
　（並列の電圧は等しくなるから）
　\(I_1=0.9×\frac{1}{3}=0.3[A]\)

③求める\(R_2\)の電圧\(V_2\)は、並列接続だから
　\(V_2=R_2×I_2=R_1×I_1\)
　　\(=R_2×0.3=90×0.3\)
　\(R_2=90×0.3÷0.3=90[Ω]\)