R4.07-2B5
R3.07-2B5
R2.01-1B5
解答
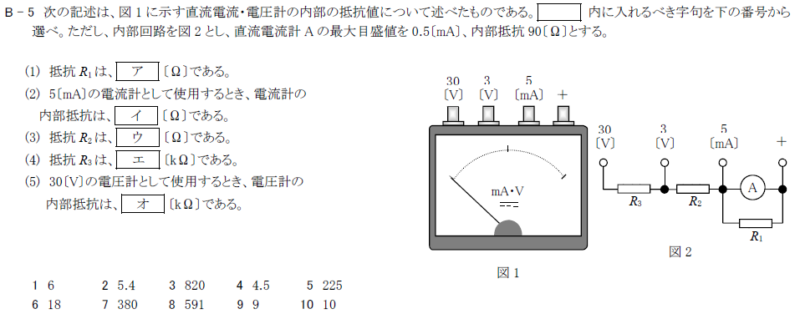
R4.07-2B5
ア 5：1
イ 9：0.9
ウ 8：599.1
エ 2：5.4
オ 6：6
ワンポイント解説
先ず、直流電流計Aの電圧\(V_A\)と\(R_1\)に流れる電流\(I_1\)を求める。
先ず、直流電流計Aの電圧\(V_A\)と\(R_1\)に流れる電流\(I_1\)を求める。
直流電流計Aの最大電流は0.5[mA]、内部抵抗は9[Ω]であるので、
\(V_A=9Ω×0.5mA=4.5mV\)
\(I_1=5mA-0.5mA=4.5mA\)
(1) 抵抗\(R_1\)は、
\(R_1=\frac{V_A}{I_1}=\frac{4.5m}{4.5m}=1[Ω]\) －ア
(2) 5[mA]の電流計として使用するとき、電流計の内部抵抗\(R\)は、
→＋端子と5[mA]端子の間に測定物を接続するので、
電流計の内部抵抗\(R_A\)と\(R_1\)の抵抗を合成したものが内部抵抗\(R\)となります。
\(R=\frac{R_A×R_1}{R_A+R_1}=\frac{9×1}{9+1}=0.9[Ω]\) －イ
(3) 抵抗\(R_2\)は、
→＋端子と3[V]端子の間に測定物を接続した場合、
電流は最大5mA、電圧は最大3Vとなり、(2)の分の抵抗を引けばよいので
\(R_2=\frac{3V}{5mA}-0.9Ω=600-0.9=599.1[Ω]\) －ウ
(4) 抵抗\(R_3\)は、
→＋端子と30[V]端子の間に測定物を接続した場合、
電流は最大5mA、電圧は最大30Vとなり、(2)と\(R_2\)の分の抵抗を引けばよいので
\(R_3=\frac{30V}{5mA}-0.9Ω-599.1Ω=6000-600=5.4k[Ω]\) －エ
(5) 30[V]の電圧計として使用するとき、電圧計の内部抵抗は、
→＋端子と30[V]端子の間に測定物を接続した場合、
内部抵抗は\(R_3+R_2+(2)の抵抗\)となるので
\(R=R_3+R_2+(2)の抵抗=5.4k+599.1+0.9=6k[Ω]\) －オ
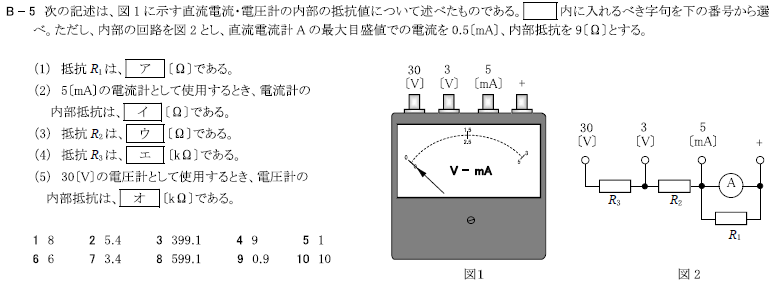
R3.07-2B5
ア 6：18
イ 7：15
ウ 8：985
エ 9：9
オ 5：10
先ず、直流電流計Aの電圧\(V_A\)と\(R_1\)に流れる電流\(I_1\)を求める。
直流電流計Aの最大電流は0.5[mA]、内部抵抗は90[Ω]であるので、
\(V_A=90Ω×0.5mA=45mV\)
\(I_1=3mA-0.5mA=2.5mA\)
(1) 抵抗\(R_1\)は、
\(R_1=\frac{V_A}{I_1}=\frac{45m}{2.5m}=18[Ω]\) －ア
(2) 3[mA]の電流計として使用するとき、電流計の内部抵抗\(R\)は、
→＋端子と3[mA]端子の間に測定物を接続するので、
電流計の内部抵抗\(R_A\)と\(R_1\)の抵抗を合成したものが内部抵抗\(R\)となります。
\(R=\frac{R_A×R_1}{R_A+R_1}=\frac{90×18}{90+18}=15[Ω]\) －イ
(3) 抵抗\(R_2\)は、
→＋端子と3[V]端子の間に測定物を接続した場合、
電流は最大3mA、電圧は最大3Vとなり、(2)の分の抵抗を引けばよいので
\(R_2=\frac{3V}{3mA}-15Ω=1000-15=985[Ω]\) －ウ
(4) 抵抗\(R_3\)は、
→＋端子と30[V]端子の間に測定物を接続した場合、
電流は最大3mA、電圧は最大30Vとなり、(2)と\(R_2\)の分の抵抗を引けばよいので
\(R_3=\frac{30V}{3mA}-15Ω-985Ω=10000-1000=9k[Ω]\) －エ
(5) 30[V]の電圧計として使用するとき、電圧計の内部抵抗は、
→＋端子と30[V]端子の間に測定物を接続した場合、
内部抵抗は\(R_3+R_2+(2)の抵抗\)となるので
\(R=R_3+R_2+(2)の抵抗=9k+985+15=10k[Ω]\) －オ
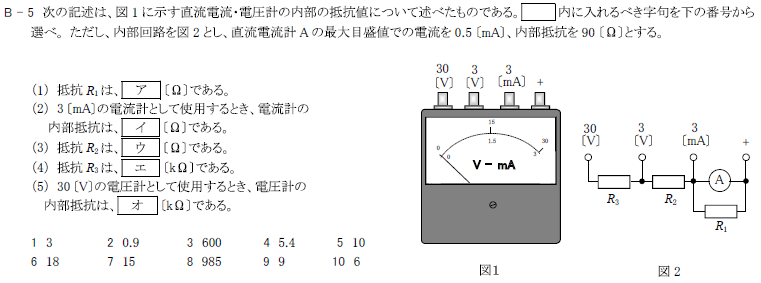
R2.01-1B5
ア 6：18
イ 2：15
ウ 8：985
エ 4：9
オ 5：10
検索用キーワード
電流・電圧計 図１に示す直流電流・電圧計の内部の抵抗値について述べたものである。 内部の回路を図２とし、直流電流計Ａの最大目盛値での電流を
コメント