基礎403

R5.07-1A9

R4.01-1A9

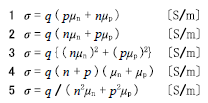
R6.01-1A9

R5.01-2A12

R3.07-2A12

R6.07-1A9

R4.07-1A9

R3.01-2A9

R2.01-1A9

解答

R5.07-1A9

\(４　σ=q(nμ_n+pμ_p)［S/m］\)

ワンポイント解説
　\(導電率σ=q(nμ_n+pμ_p)［S/m］\)
　導電率なんでどうでもいいだろ～は（\(σ=\)）　急に（\(q\)）　ローマ字読みでヌンププ（nun　pup）

R4.01-1A9

\(２　σ=q(nμ_n+pμ_p)［S/m］\)

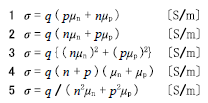
R6.01-1A9

４　0.2［㎡/(V・s)］

ワンポイント解説
　\(I=\frac{SμVρe}{l}\)
　電流は（\(I=\)）、SUV（\(SμV\)）のロエ（\(ρe\)）に乗るが、長さ（\(l\)）で悪い（÷）
　\(e=q=電荷\)
　　\(I\)：電流[A]
　　\(S\)：断面積[㎡]
　　\(μ\)：移動度［㎡/(V・s)］
　　\(V\)：電圧[V]
　　\(ρ\)：密度[個/㎥]
　　\(e\)：電荷[C]

\(I=\frac{SμVρe}{l}\)より、
移動度\(μ=\frac{Il}{SVρe}\)より、
　\(=\frac{16m×20m}{2m^2×5×1×10^{21}×1.6×10^{-19}}=\frac{20m}{10^2}=0.2\)［㎡/(V・s)］
※\(1[㎟]=1[㎜]×1[㎜]=0.001[m]×0.001[m]=10^{-6}[㎡]=1m^2[㎡]\)なので
　\(2[㎟]=2m^2[㎡]\)

R5.01-2A12

１　25.6［mA］

ワンポイント解説
　\(I=\frac{SμVρe}{l}\)
　電流は（\(I=\)）、SUV（\(SμV\)）のロエ（\(ρe\)）に乗るが、長さ（\(l\)）で悪い（÷）
　\(e=q=電荷\)

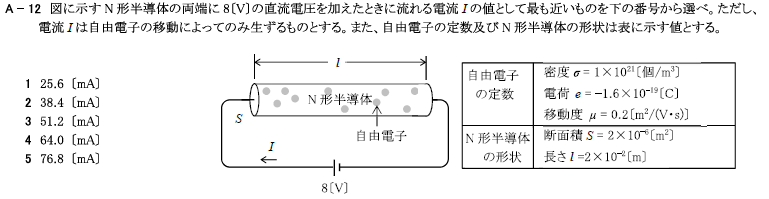
\(I=\frac{SμVρe}{l}=\frac{2×10^{-6}×0.2×8×1×10^{21}×-1.6×10^{-19}}{2×10^{-2}}\)　※マイナスは無視します。
　\(=\frac{2×0.2×8×1.6×10^{-6}×10^{21}×10^{-19}×10^{2}}{2}=\frac{5.12×10^{-2}}{2}=2.56×10^{-2}=25.6\)[mA]

R3.07-2A12

２　25.6［mA］

R6.07-1A9

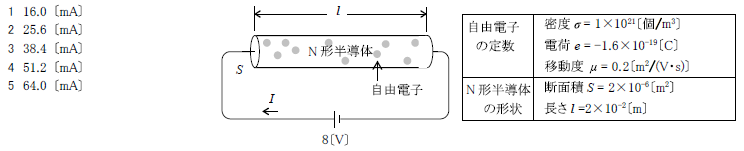
\(１　I=\frac{Sμ_nσqV}{l}\)

ワンポイント解説
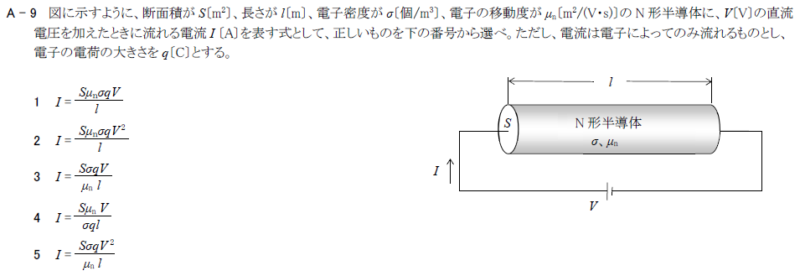
　\(I=\frac{Sμ_nσqV}{l}\)
　電流は（\(I=\)）、SUV（\(SμV\)）に乗るが、老朽（\(σq\)）化している。

R4.07-1A9

\(４　I=\frac{Sμ_nσqV}{l}\)

R3.01-2A9

\(５　I=\frac{Sμ_nσqV}{l}\)

R2.01-1A9

\(５　I=\frac{Sμ_nσqV}{l}\)

検索用キーワード（問題文の最初の一文）

電子密度及びホール（正孔）密度がそれぞれn[1/㎥]及びp[1/㎥]である半導体の導電率σを表す式
図に示すＮ形半導体の両端に8[V]の直流電圧を加えたときに流れる電流Iの値
図に示すように、断面積がS[㎡]、長さがl[m]、電子密度がσ[個/㎥]、電子の移動度が\(μ_n\)[㎡/(V・s)]のＮ形半導体に、V[V]の直流電圧を加えたときに流れる電流I[A]を表す式
Ｎ形半導体の両端に5[V]の直流電圧を加えたとき、16[mA]の電流が流れた。このときの自由電子の移動度の値