R6.01-1A8
R4.07-2A8
解答
R6.01-1A8
1 3.6[mH] 0.01[μF] 0.015[μF]
ワンポイント解説
逆回路のルール
①直列L → 並列C
直列C → 並列L
並列L → 直列C
並列C → 直列L
②変換後のL、Cの値は、\(\frac{L}{C}=R^2\)の関係となる。
\(Z_1=jωL、Z_2=\frac{1}{jωC}\)とすると、
\(Z_1Z_2=jωL×\frac{1}{jωC}=\frac{L}{C}=R^2\)
逆回路のルールより、(図2→図3で考えます。)
・\(L_A\)は\(C_0\)との直列接続なので、図3の並列接続の\(C_1\)になる。
\(\frac{L}{C}=R^2\)より、
\(C_1=\frac{L_A}{R^2}=\frac{3.6m}{600^2}=\frac{3.6×^{-3}}{36×10^{4}}=0.1×10^{-7}=0.01\)[μF]
・\(C_0\)は\(L_A\)との直列接続なので、図3の並列接続の\(L_1\)になる。
\(L_1=C_0R^2=0.01μ×600^2=10^{-8}×36×10^4=3.6×10^{-3}=3.6\)[mH]
・\(L_B\)は\(L_A、C_0\)との並列接続なので、図3の直列接続の\(C_2\)になる。
\(C_2=\frac{L}{R^2}=\frac{5.4m}{600^2}=\frac{5.4×10^{-3}}{36×10^4}=\frac{3}{2}×10^{-8}=0.015\)[μF]
R4.07-2A8
4 0.01[μF] 3.6[mH] 0.015[μF]

解き方は同上です。選択肢を並び替えただけですね。
検索用キーワード(問題文の最初の一文)
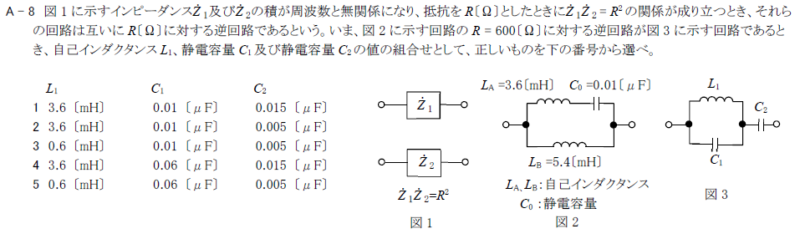
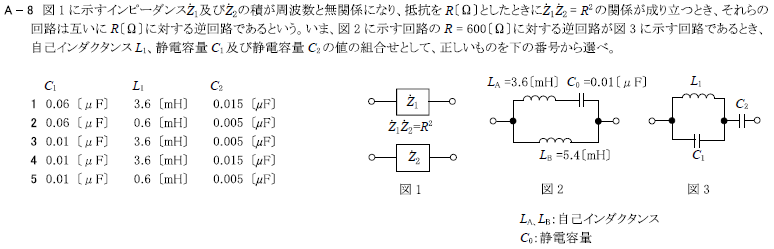
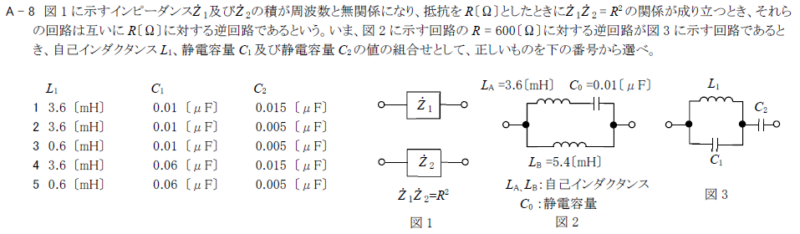
図1に示すインピーダンス\(\dot{Z}_1\)及び\(\dot{Z}_2\)の積が周波数と無関係になり、抵抗を\(R\)[Ω]としたときに\(\dot{Z}_1\dot{Z}_2=R^2\)の関係が成り立つとき、それらの回路は互いに\(R\)[Ω]に対する逆回路であるという。いま、図2に示す回路の\(R=600\)[Ω]に対する逆回路が図3に示す回路であるとき、自己インダクタンス\(L_1\)、静電容量\(C_1\)及び静電容量\(C_2\)の値


コメント