R6.07-1A6

R6.01-1A6
R5.07-2A8
R5.01-2A6

R3.07-1A8
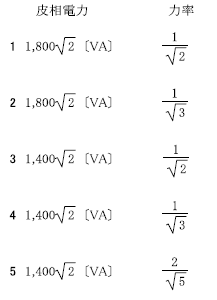
R1.07-1A6
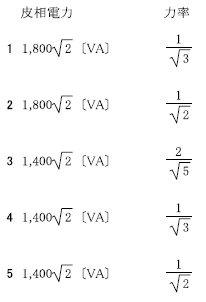
R4.01-1A8
R3.07-2A6
R3.01-1A8
解答
R6.07-1A6
\(2 500\sqrt{5}[VA] \frac{2}{\sqrt{5}}\)
ワンポイント解説
(1)各電力ベクトルを図で確認
※容量性(\(-j\frac{1}{ωC}\))は下向き、誘導性(\(+jωL\))は上向き
(2)電力合成ベクトルを作図 ※上向きは遅れ、下向きは進み
(3)回路電流\(\dot{I}=\frac{皮相電力}{交流電源電圧}\)
\(力率=\frac{有効電力}{皮相電力}\)

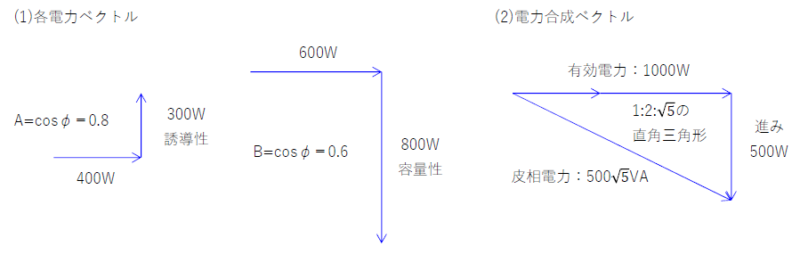
(3)(2)図より回路の皮相電力は、\(500\sqrt{5}\)[VA]である。
\(力率=\frac{有効電力}{皮相電力}=\frac{1000}{500\sqrt{5}}=\frac{2}{\sqrt{5}}\)
R6.01-1A6
\(2 700\sqrt{5}[VA] \frac{2}{\sqrt{5}}\)

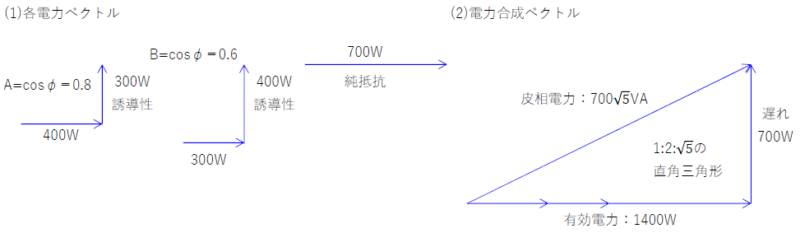
(3)(2)図より回路の皮相電力は、\(700\sqrt{5}\)[VA]である。
\(力率=\frac{有効電力}{皮相電力}=\frac{1400}{700\sqrt{5}}=\frac{2}{\sqrt{5}}\)
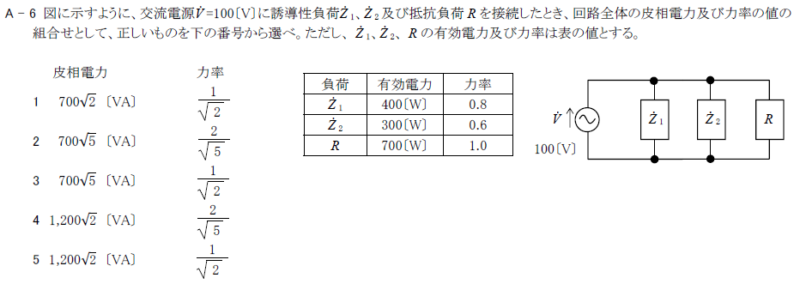
R5.07-2A8
\(4 1,300[VA] \frac{12}{13}\)

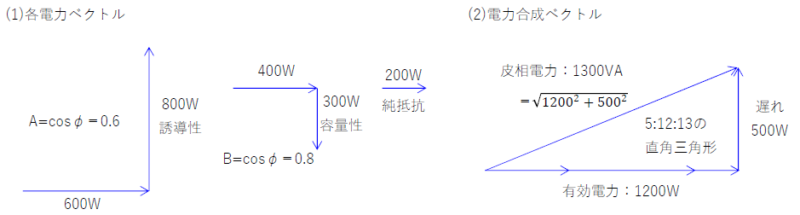
(3)(2)図より回路の皮相電力は、\(1300\)[VA]である。
\(力率=\frac{有効電力}{皮相電力}=\frac{1200}{1300}=\frac{12}{13}\)
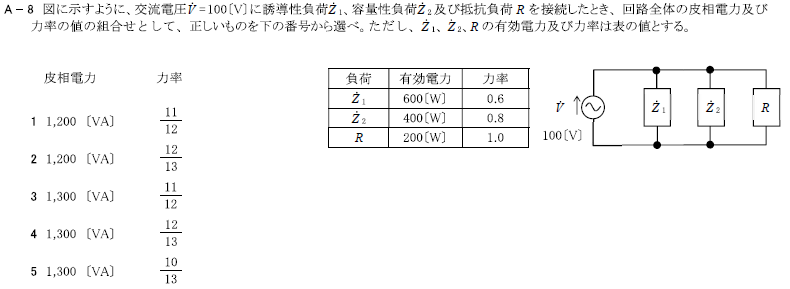
R5.01-2A6
\(1 1,400\sqrt{2}[VA] \frac{1}{\sqrt{2}}\)

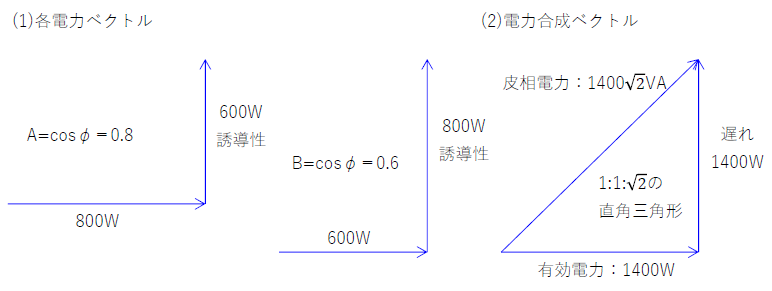
(3)(2)図より回路の皮相電力は、\(1400\sqrt{2}\)[VA]である。
\(力率=\frac{有効電力}{皮相電力}=\frac{1400}{1400\sqrt{2}}=\frac{1}{\sqrt{2}}\)
R3.07-1A8
\(3 1,400\sqrt{2}[VA] \frac{1}{\sqrt{2}}\)
R1.07-1A6
\(5 1,400\sqrt{2}[VA] \frac{1}{\sqrt{2}}\)
R4.01-1A8
\(3 1,300[VA] \frac{12}{13}\)
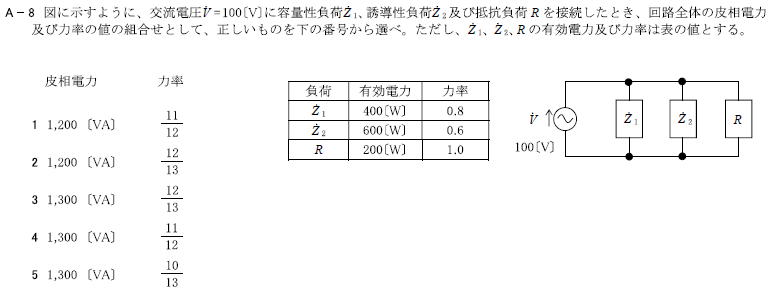
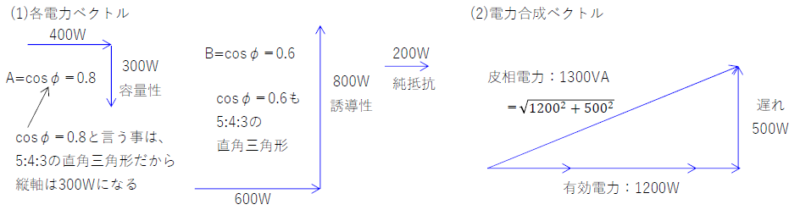
(3)(2)図より回路の皮相電力は、\(1300\)[VA]である。
\(力率=\frac{有効電力}{皮相電力}=\frac{1200}{1300}=\frac{12}{13}\)
R3.07-2A6
\(3 700\sqrt{5}[VA] \frac{2}{\sqrt{5}}\)
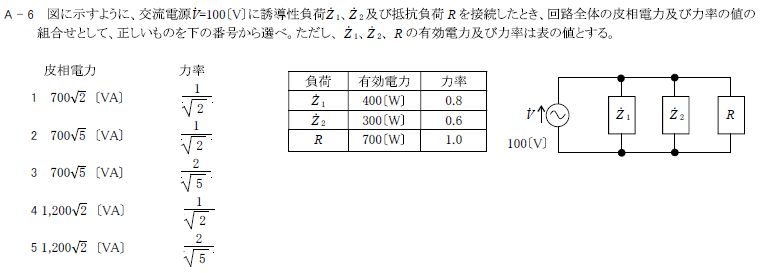

(3)(2)図より回路の皮相電力は、\(700\sqrt{5}\)[VA]である。
\(力率=\frac{有効電力}{皮相電力}=\frac{1400}{700\sqrt{5}}=\frac{2}{\sqrt{5}}\)
R3.01-1A8
\(3 600\sqrt{5}[VA] \frac{2}{\sqrt{5}}\)

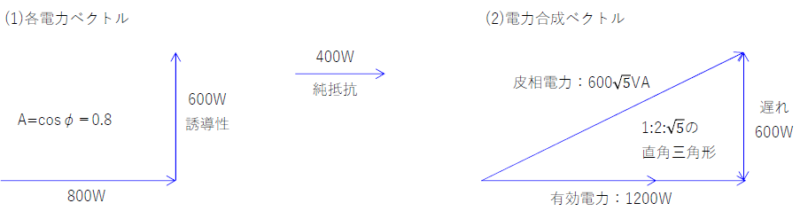
(3)(2)図より回路の皮相電力は、\(600\sqrt{5}\)[VA]である。
\(力率=\frac{有効電力}{皮相電力}=\frac{1200}{600\sqrt{5}}=\frac{2}{\sqrt{5}}\)
検索用キーワード(問題文の最初の一文)
交流電圧\(\dot{V}=100\)[V]に誘導性負荷\(\dot{Z}_1\)[Ω]及び容量性負荷\(\dot{Z}_2\)[Ω]を接続したとき、回路全体の皮相電力及び力率の値
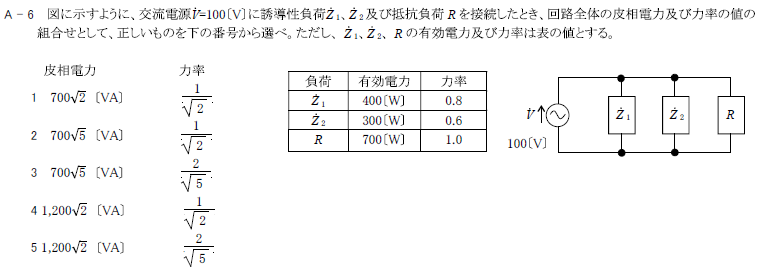
交流電圧\(\dot{V}=100\)[V]に誘導性負荷\(\dot{Z}_1\)、容量性負荷\(\dot{Z}_2\)及び抵抗負荷\(R\)を接続したとき、回路全体の皮相電力及び力率の値
交流電源電圧\(\dot{V}=100\)[V]に誘導性負荷\(\dot{Z}_1\)及び\(\dot{Z}_2\)を接続したとき、回路全体の皮相電力及び力率の値
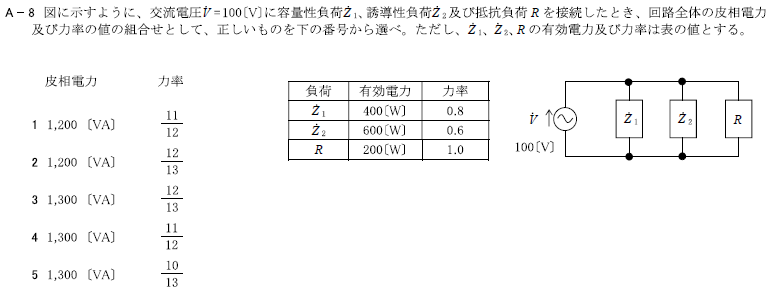
交流電圧\(\dot{V}=100\)[V]に容量性負荷\(\dot{Z}_1\)、誘導性負荷\(\dot{Z}_2\)及び抵抗負荷\(R\)を接続したとき、回路全体の皮相電力及び力率の値
交流電源\(\dot{V}=100\)[V]に誘導性負荷\(\dot{Z}_1\)、\(\dot{Z}_2\)及び抵抗負荷\(R\)を接続したとき、回路全体の皮相電力及び力率の値
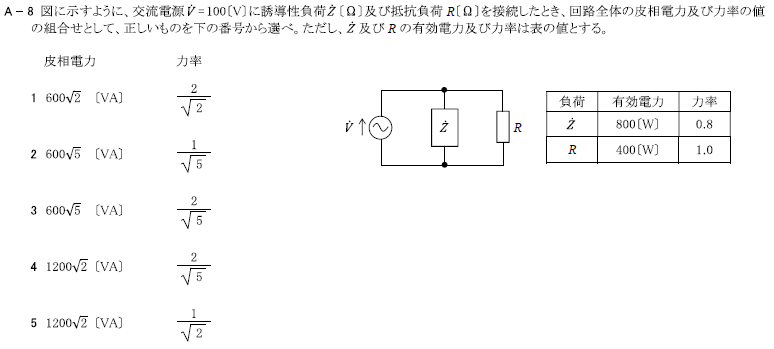
交流電源\(\dot{V}=100\)[V]に誘導性負荷\(\dot{Z}\)及び抵抗負荷\(R\)を接続したとき、回路全体の皮相電力及び力率の値


コメント