基礎1204

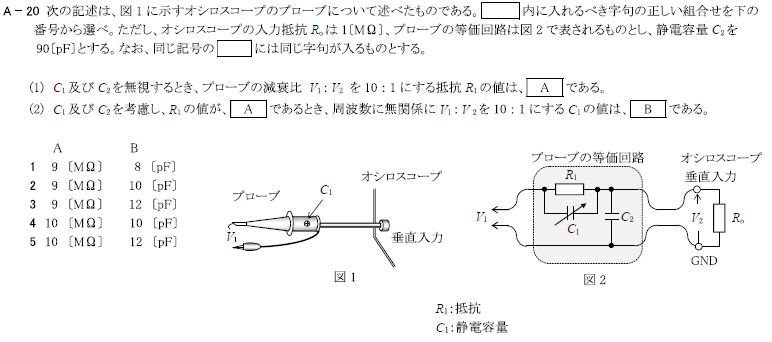
R5.07-1A20

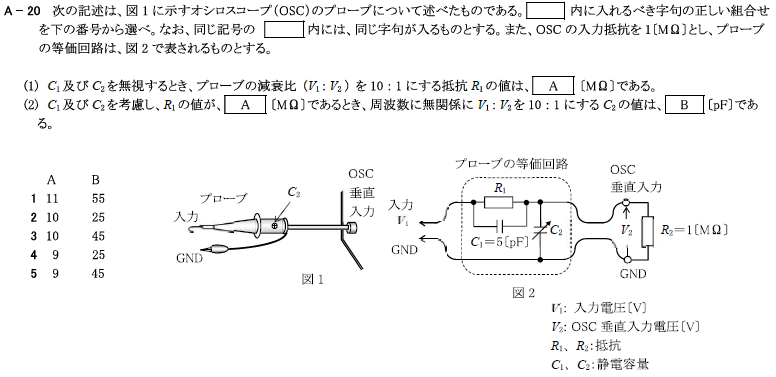
R4.01-1A20

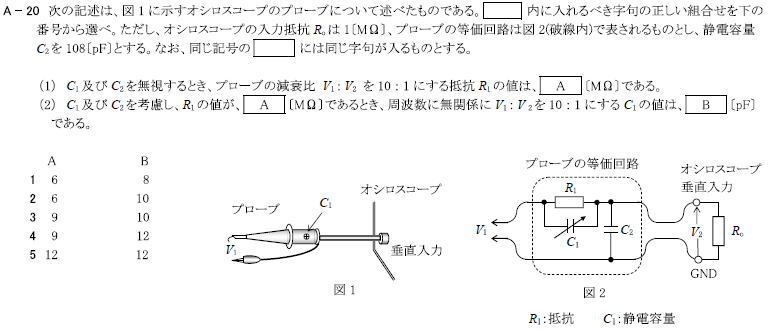
R2.11-1A20

解答

R5.07-1A20

５　9　　　45

ワンポイント解説
プローブの抵抗とコンデンサの式　※\(V_1:V_2=10:1\)に限る
　\(R_1=9R_2\)　プローブの抵抗（R）は良い国（192）
　　\(R_1\)：等価回路内の抵抗　　\(R_2\)：オシロスコープの抵抗
　\(C_2=9C_1\)　コンデンサ（C）は憎い（291）

(1)\(R_1=9R_2\)より、
　\(R_1=9×1=9[MΩ]\)
(2)\(C_2=9C_1\)より、
　\(C_2=9C_1=9×5=45[pF]\)

R4.01-1A20

４　9　　　12

(1)\(R_1=9R_2\)より、
　\(R_1=9×1=9[MΩ]\)
(2)\(C_2=9C_1\)より、
　\(C_1=\frac{C_2}{9}=\frac{108}{9}=12[pF]\)

R2.11-1A20

２　9［MΩ］　　　10［pF］

(1)\(R_1=9R_2\)より、
　\(R_1=9×1=9[MΩ]\)
(2)\(C_2=9C_1\)より、
　\(C_1=\frac{C_2}{9}=\frac{90}{9}=10[pF]\)

ワンポイント解説

(1)\(C_1\)及び\(C_2\)を無視するとき、プローブの減衰比\(V_1:V_2\)を\(10:1\)にする抵抗\(R_1\)の値は、（　　　）である。

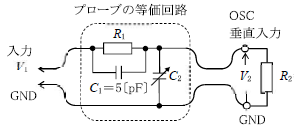
\(C_1\)及び\(C_2\)を無視するとき、　→\(R_1\)と\(R_2\)の直列接続と見なせるので\(V_2\)は、
　\(V_2=V_1×\frac{R_2}{R_1+R_2}\)より、
　\(\frac{V_1}{V_2}=\frac{R_1+R_2}{R_2}\)
プローブの減衰比\(V_1:V_2\)を\(10:1\)にする抵抗\(R_1\)の値は、
　\(\frac{V_1}{V_2}=\frac{R_1+R_2}{R_2}=\frac{10}{1}\)　※\(V_1:V_2=10:1\)
　\(R_1+R_2=10R_2\)
　\(R_1=9R_2\)

(2)\(C_1\)及び\(C_2\)を考慮し、\(R_1\)の値が、\(R_1=9R_2\)[MΩ]であるとき、周波数に無関係に\(V_1:V_2\)を\(10:1\)にする\(C_2\)の値は、（　　　）[pF]である。

\(C_1\)及び\(C_2\)を考慮し、　→\(R_1\)と\(C_1\)のインピーダンスを\(Z_1\)、\(R_2\)と\(C_2\)のインピーダンスを\(Z_2\)とすると
　\(Z_1=\frac{R_1×\frac{1}{jωC_1}}{R_1+\frac{1}{jωC_1}}\)
　\(Z_2=\frac{R_2×\frac{1}{jωC_2}}{R_2+\frac{1}{jωC_2}}\)
プローブの減衰比を考えます。(1)より\(V_1:V_2=10:1\)なので、電圧は10:1。抵抗（インピーダンス）は\(R_1:R_2=9:1=Z_1:Z_2\)となるので、
　\(Z_1=9Z_2\)
　\(\frac{R_1×\frac{1}{jωC_1}}{R_1+\frac{1}{jωC_1}}=9\frac{R_2×\frac{1}{jωC_2}}{R_2+\frac{1}{jωC_2}}\)
　\(\frac{R_1}{1+jωC_1R_1}=9\frac{R_2}{1+jωC_2R_2}\)
　\(\frac{1+jωC_2R_2}{1+jωC_1R_1}=\frac{9R_2}{R_1}\)
\(R_1=9R_2\)より、
　\(\frac{1+jωC_2R_2}{1+jωC_1R_1}=\frac{9R_2}{9R_2}=1\)
　よって左辺の虚数部は等しくなるので
　\(ωC_2R_2=ωC_1R_1\)
\(C_2=\frac{C_1R_1}{R_2}=\frac{C_1×9R_2}{R_2}=9C_1\)

検索用キーワード

プローブ　図１に示すオシロスコープ（OSC）のプローブについて述べたものである。