R7.01-1A19

R5.07-2A19

R2.11-1A19

R4.01-1A19

H31.01-1A19

解答
R7.01-1A19
4 3[pF]
ワンポイント解説
\(C_O\)の公式
\(C_O=\frac{C_{S1}+4C_{S2}}{3}\)

\(C_O=\frac{C_{S1}+4C_{S2}}{3}=\frac{457-4×112}{3}=\frac{9}{3}=3[pF]\)
R5.07-2A19
5 3[pF]

\(C_O=\frac{C_{S1}+4C_{S2}}{3}=\frac{457-4×112}{3}=\frac{9}{3}=3[pF]\)
R2.11-1A19
1 3[pF]
R4.01-1A19
1 6[pF]
ワンポイント解説
\(C_O\)の公式
\(C_O=\frac{C_{S1}+4C_{S2}}{3}\)

\(C_O=\frac{C_{S1}+4C_{S2}}{3}=\frac{426-4×102}{3}=\frac{18}{3}=6[pF]\)
H31.01-1A19
3 6[pF]
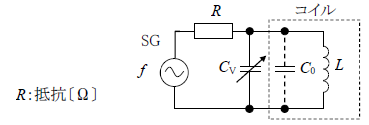
この図形の答えは、6[pF]か3[pF]なのでしょうか?
ワンポイント解説
\(C_O\)の公式は、共振条件より
\(f_1\)のとき、\(ω_1L=\frac{1}{ω_1(C_O+C_{S1})}\) -①
\(f_2\)のとき、\(ω_2L=\frac{1}{ω_2(C_O+C_{S2})}\) -②
②÷①より、
\(\frac{ω_2}{ω_1}=\frac{ω_1(C_O+C_{S1})}{ω_2(C_O+C_{S2})}\)
\((\frac{ω_2}{ω_1})^2=\frac{C_O+C_{S1}}{C_O+C_{S2}}=(\frac{f_2}{f_1})^2\) -③
\(f_2=2f_1\)のとき、③式は、\(\frac{C_O+C_{S1}}{C_O+C_{S2}}=(\frac{f_2}{f_1})^2=4\)
\(C_O+C_{S1}=4C_O+4C_{S2}\)
\(3C_O=C_{S1}-4C_{S2}\)
よって、
\(C_O=\frac{C_{S1}-4C_{S2}}{3}\)
検索用キーワード(問題文の最初の一文)
標準信号発生器SGの周波数fを200[kHz]にしたとき可変静電容量\(C_V\)が457[pF]で回路が共振し、
fを400[kHz]にしたとき\(C_v\)が112[pF]で回路が共振した。このとき自己インダクタンスがL[H]のコイルの分布容量\(C_0\)の値
発振器SGの周波数fを300[kHz]にしたとき可変静電容量\(C_V\)が426[pF]で回路が共振し、
fを600[kHz]にしたとき\(C_v\)が102[pF]で回路が共振した。このとき自己インダクタンスがL[H]のコイルの分布容量\(C_0\)の値


コメント