基礎1105(2)

R5.01-2A19

解答

R5.01-2A19

\(３　\frac{C_X}{C_0}=\frac{R_2}{R_1}-\frac{R_0}{R_X}\)

ワンポイント解説
　左上から右下に小文字のみで覚えてしまいましょう。
　X　２　０　０　１　X　－（エックス２００１エックス　マイナスで）

解説

ポイント
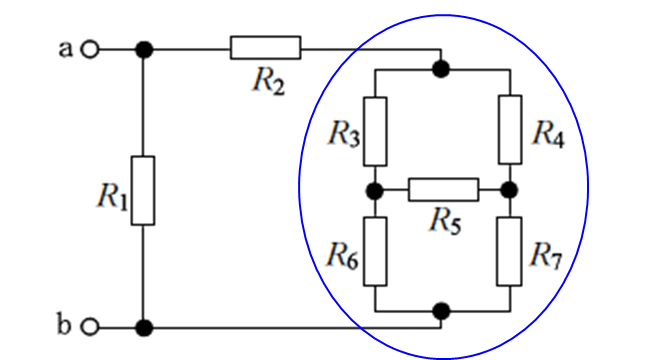
　この形はブリッジの合成抵抗の問題
　　対角線の抵抗の積
　　　\(R_3×R_7=R_4×R_6\)　ならば
　平衡状態で\(R_5\)は無視出来る。

ブリッジ回路の平衡条件より、
　\(R_1×(R_0+\frac{1}{jωC_0})=R_2×\frac{R_X×\frac{1}{jωC_X}}{R_X+\frac{1}{jωC_X}}\)
右辺の分数を整理すると
　\(R_1×(R_0+\frac{1}{jωC_0})=R_2×\frac{R_X}{1+jωC_XR_X}\)
両辺に、\(1+jωC_XR_X\)をかけて
　\(R_1×(R_0+\frac{1}{jωC_0})(1+jωC_XR_X)=R_2×\frac{R_X}{1+jωC_XR_X}×(1+jωC_XR_X)\)
　\((R_0+\frac{1}{jωC_0})(1+jωC_XR_X)=\frac{R_2R_X}{R_1}\)
　\(\frac{R_2R_X}{R_1}=(R_0+\frac{1}{jωC_0})(1+jωC_XR_X)\)
右辺を展開して
　\(\frac{R_2R_X}{R_1}=R_0+jωC_XR_XR_0+\frac{1}{jωC_0}+\frac{jωC_XR_X}{jωC_0}\)
　\(\frac{R_2R_X}{R_1}=R_0+\frac{C_XR_X}{C_0}+j(ωC_XR_XR_0-\frac{1}{ωC_0})\)　－①
ここで、実数部は等しくなるため、
　\(\frac{R_2R_X}{R_1}=R_0+\frac{C_XR_X}{C_0}\)
また、\(\frac{C_X}{C_0}\)について整理すると
　\(\frac{C_XR_X}{C_0}=\frac{R_2R_X}{R_1}-R_0\)
　\(\frac{C_X}{C_0}=\frac{R_2R_X}{R_1R_X}-\frac{R_0}{R_X}=\frac{R_2}{R_1}-\frac{R_0}{R_X}\)

延長戦です。
問題文に\(ωC_XR_X=1/ωC_0R_0\)が成立する条件と言うのは
①の式のjパートは0になるから、実数部のみを考えれば良い。と言う事です。
\(ωC_XR_XR_0-\frac{1}{ωC_0}=\frac{R_0}{ωC_0R_0}-\frac{1}{ωC_0}=0\)

検索用キーワード

シェーリングブリッジ　図に示すブリッジで静電容量　平衡条件