基礎1101

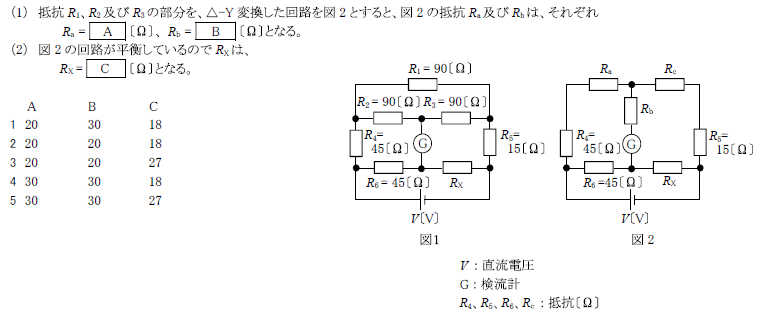
R5.07-1A5

R3.07-2A5

R2.01-1A5

解答

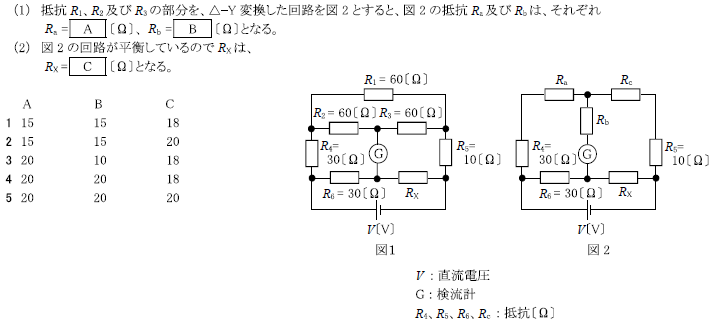
R5.07-1A5

２　30　　　30　　　27

Δ（デルタ）Ｙ（スター）変換

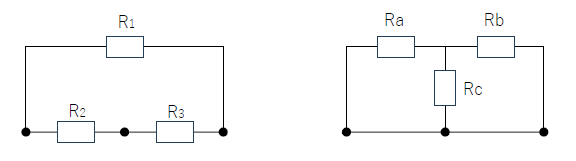
　Δ回路、Ｙ回路の各抵抗値は、以下の式で表されます。
　\(R_a=\frac{R_2R_3}{R_1+R_2+R_3}\)
　\(R_b=\frac{R_1R_3}{R_1+R_2+R_3}\)
　\(R_c=\frac{R_1R_2}{R_1+R_2+R_3}\)
　※過去問では、\(R_1\),\(R_2\),\(R_3\)は同じ値が出題されています。
　　分母が３つ全ての足し算、分子は抵抗２つの掛け算です。

(1)\(R_a=\frac{R_2R_3}{R_1+R_2+R_3}\)
　\(R_a=\frac{90×90}{90+90+90}=\frac{8100}{270}=30\)[Ω]

　\(R_b\)は、\(R_1\)、\(R_2\)、\(R_3\)共に同じ90[Ω]なので、
　\(R_b=30\)[Ω]

(2)図2のブリッジの平衡条件により、

ポイント
　この形はブリッジの平衡問題
　　対角線の抵抗の積
　　　\(R_3×R_7=R_4×R_6\)　ならば
　平衡状態で\(R_5\)は無視出来る。

　\((R_a+R_4)×R_X=(R_c+R_5)×R_6\)
　\(R_X=\frac{(R_c+R_5)×R_6}{R_a+R_4}=\frac{(30+15)×45}{30+45}=\frac{45×45}{75}=27\)[Ω]

R3.07-2A5

５　30　　　30　　　27

R2.01-1A5

４　20　　　20　　　18

(1)\(R_a=\frac{R_2R_3}{R_1+R_2+R_3}\)
　\(R_a=\frac{60×60}{60+60+60}=\frac{3600}{180}=20\)[Ω]

　\(R_b\)は、\(R_1\)、\(R_2\)、\(R_3\)共に同じ60[Ω]なので、
　\(R_b=20\)[Ω]

(2)図2のブリッジの平衡条件により、
　\((R_a+R_4)×R_X=(R_c+R_5)×R_6\)
　\(R_X=\frac{(R_c+R_5)×R_6}{R_a+R_4}=\frac{(20+10)×30}{20+30}=\frac{30×30}{50}=18\)[Ω]

検索用キーワード

直流ブリッジ（Δ－Y変換）　図１に示すブリッジ回路によって、抵抗\(R_X\)を求める過程について述べたものである。　平衡