R6.07-1A15
R3.01-2A15
解答
R6.07-1A15
5 10[kHz]
ワンポイント解説
負帰還増幅回路の高域遮断周波数\(F_H=f_H(1+βA)\)
\(f_H\):Ampの高域遮断周波数 \(β\):帰還率 \(A\):Ampの利得(真数)

①数値を整理
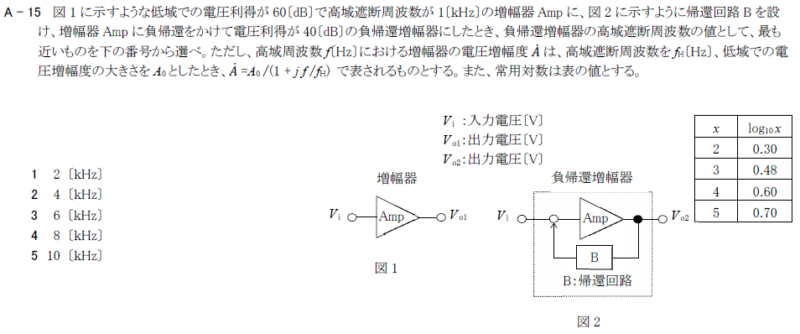
・図1 Ampの「電圧」利得\(A=60\)[dB]、高域遮断周波数\(f_H=1\)[kHz]
・図2 負帰還増幅回路の「電圧」利得\(A_β=40\)[dB]、高域遮断周波数\(F_H\)を求める。
②\(β\)は図2の負帰還増幅器の電圧利得の式\(A_β=\frac{A}{1+βA}\)から求める。※\(A_βとA\)は真数
\(A_β=\frac{A}{1+βA}\)
\(1+βA=\frac{A}{A_β}\)
\(β=\frac{1}{A_β}-\frac{1}{A}\)
デシベル計算 ※電圧は2倍
+10dB=10倍 +3dB=2倍
-10dB=1/10倍 -3dB=1/2倍
\(A=60[dB]\)←電圧は2倍されているから、\(A=30[dB]\)の真数を求める。
\(A=30[dB]=10[dB]+10[dB]+10[dB]\)
\(=10×10×10=1,000\)
\(A_β=40[dB]\)←電圧は2倍されているから、\(A_β=20[dB]\)の真数を求める。
\(A_β=20[dB]=10[dB]+10[dB]\)
\(=10×10=100\)
\(A=1,000、A_β=100\)
\(β=\frac{1}{A_β}-\frac{1}{A}=\frac{1}{100}-\frac{1}{1,000}\)
\(=0.01-0.001=0.009=9×10^{-3}\)
③公式に代入
負帰還増幅回路の高域遮断周波数\(F_H=f_H(1+βA)\)
\(=1×10^{3}(1+9×10^{-3}×1,000)\)
\(=1×10^{3}(1+9)=10×10^{3}=10\)[kHz]
R3.01-2A15
1 40[kHz]

①数値を整理
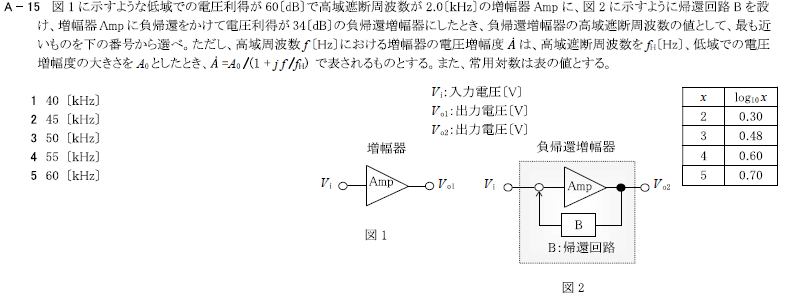
・図1 Ampの「電圧」利得\(A=60\)[dB]、高域遮断周波数\(f_H=2.0\)[kHz]
・図2 負帰還増幅回路の「電圧」利得\(A_β=34\)[dB]、高域遮断周波数\(F_H\)を求める。
②\(β\)は図2の負帰還増幅器の電圧利得の式\(A_β=\frac{A}{1+βA}\)から求める。※\(A_βとA\)は真数
\(A_β=\frac{A}{1+βA}\)
\(1+βA=\frac{A}{A_β}\)
\(β=\frac{1}{A_β}-\frac{1}{A}\)
デシベル計算 ※電圧は2倍
+10dB=10倍 +3dB=2倍
-10dB=1/10倍 -3dB=1/2倍
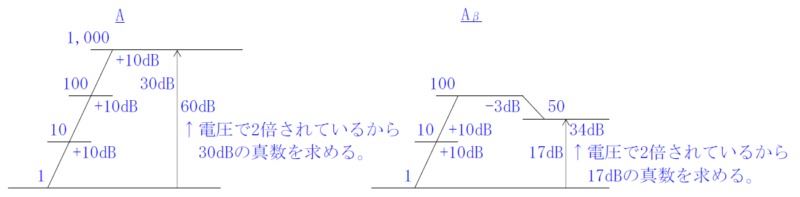
\(A=1,000、A_β=50\)
\(β=\frac{1}{A_β}-\frac{1}{A}=\frac{1}{50}-\frac{1}{1,000}\)
\(=0.02-0.001=0.019=19×10^{-3}\)
③公式に代入
負帰還増幅回路の高域遮断周波数\(F_H=f_H(1+βA)\)
\(=2×10^{3}(1+19×10^{-3}×1,000)\)
\(=2×10^{3}(1+19)=40×10^{3}=40\)[kHz]
検索用キーワード(問題文の最初の一文)
図1に示すような低域での電圧利得が60[dB]で高域遮断周波数が1.0[kHz]の増幅器Ampに、図2に示すように帰還回路Bを設け、増幅器Ampに負帰還をかけて電圧利得が40[dB]の負帰還増幅器にしたとき、負帰還増幅器の高域遮断周波数の値
図1に示すような低域での電圧利得が60[dB]で高域遮断周波数が2.0[kHz]の増幅器Ampに、図2に示すように帰還回路Bを設け、増幅器Ampに負帰還をかけて電圧利得が34[dB]の負帰還増幅器にしたとき、負帰還増幅器の高域遮断周波数の値


コメント