基礎305

R4.01-2A8

R2.11-1A8

解答

R4.01-2A8

３　\(\frac{1}{\sqrt{2}}\)

ワンポイント解説
　図を書いて整理する。

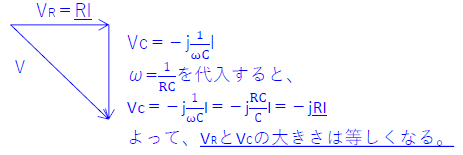
上の図は、\(V_R\)と\(V_C\)が等しいから、1：1：\(\sqrt{2}\)の三角形になる。
\(｜V_C｜=1\)
\(｜V｜=\sqrt{2}\)
\(\frac{｜V_C｜}{｜V｜}=\frac{1}{\sqrt{2}}\)

R2.11-1A8

３　\(\frac{1}{\sqrt{2}}\)

上の図は、\(V_R\)と\(V_L\)が等しいから、1：1：\(\sqrt{2}\)の三角形になる。
\(｜V_L｜=1\)
\(｜V｜=\sqrt{2}\)
\(\frac{｜V_L｜}{｜V｜}=\frac{1}{\sqrt{2}}\)

検索用キーワード（問題文の最初の一文）

図に示す抵抗R[Ω]及び静電容量C[F]の回路において、電源電圧V[V]の角周波数ωが、ω=1/(RC)[rad/s]であるとき、Cの両端電圧VcとVの大きさの比の値（|Vc|/|V|）
図に示す抵抗R[Ω]及び自己インダクタンスL[H]の回路において、電源電圧V[V]の角周波数ωが、ω=R/L[rad/s]であるとき、Lの両端電圧VLとVの大きさの比の値（|VL|/|V|）