R4.07-2A19
R6.07-1A19
R4.01-2A19
R2.01-1A18
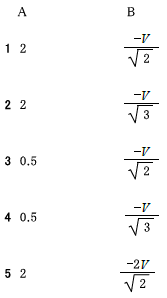
R3.01-2A20
解答
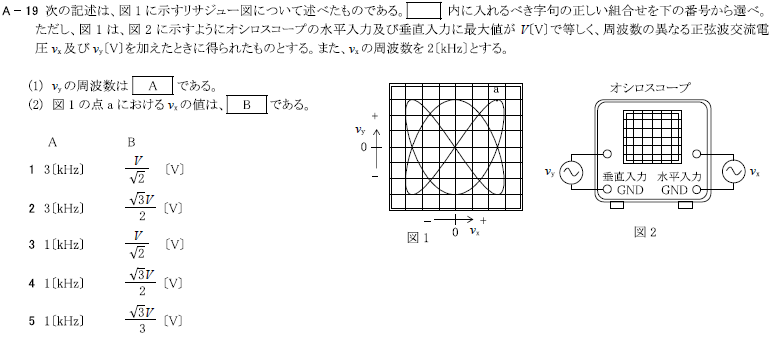
R4.07-2A19
\(2 3[kHz] \frac{\sqrt{3}V}{2}[V]\)

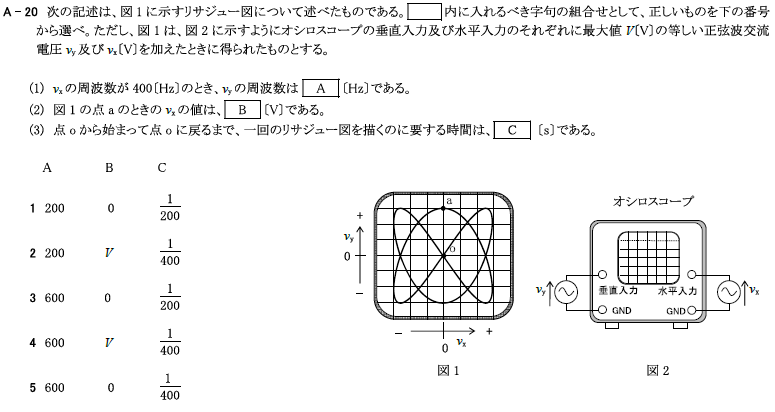
(1)\(V_x\)と\(V_y\)の周波数比をピークの数から求める
X軸方向に増減が変化するピーク数(〇)は4、Y軸方向に増減が変化するピーク数(〇)は6
\(x:y=4:6=2:3 2y=3x y=\frac{3}{2}x\)
\(x=2kのとき、y=\frac{3}{2}×2k=3k=3[kHz]\)
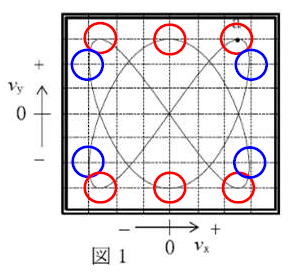
(2)下図より、
a点はY軸のピークだから、Y軸のa点の位相\(θ_y=\frac{π}{2}\)
\(V_x\)のa点の位相\(θ_x\)は、\(x:y=2:3\)より、
\(θ_x=\frac{2}{3}θ_y=\frac{2}{3}×\frac{π}{2}=\frac{π}{3}\)
\(V_x=V\sin{θ_x}=V\sin{\frac{π}{3}}=\frac{\sqrt{3}V}{2}\)
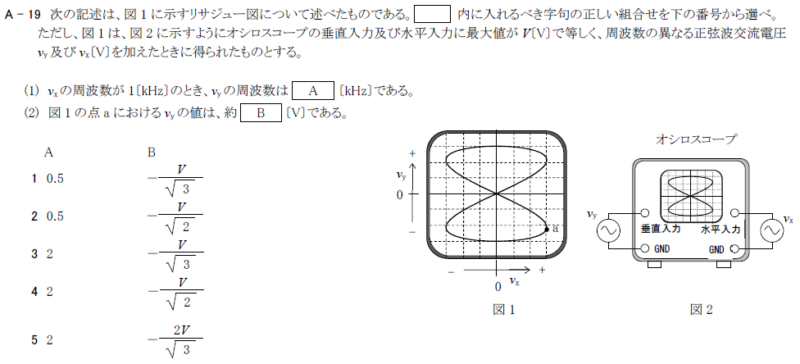
R6.07-1A19
\(2 0.5[kHz] -\frac{V}{\sqrt{2}}[V]\)

(1)\(V_x\)と\(V_y\)の周波数比をピークの数から求める
X軸方向に増減が変化するピーク数は4、Y軸方向に増減が変化するピーク数は2
\(x:y=4:2=2:1 2y=1x y=\frac{x}{2}\)
\(x=1kのとき、y=\frac{1}{2}×1k=0.5k=0.5[kHz]\)
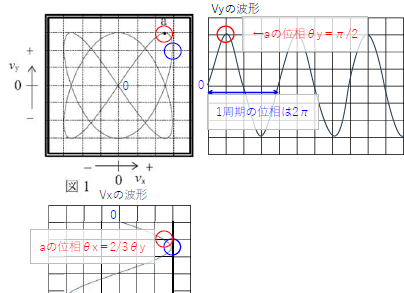
(2)a点はX軸のピークだから、
X軸のa点の位相\(θ_x=2π+\frac{π}{2}=\frac{4π+π}{2}=\frac{5π}{2}\)
\(V_y\)のa点の位相\(θ_y\)は、\(x:y=2:1\)より、
\(θ_y=\frac{θ_x}{2}=\frac{5π}{2}×\frac{1}{2}=\frac{5π}{4}=π+\frac{π}{4}\)
\(V_x=V\sin{θ_x}=V\sin{(π+\frac{π}{4})}=\frac{-V}{\sqrt{2}}\)
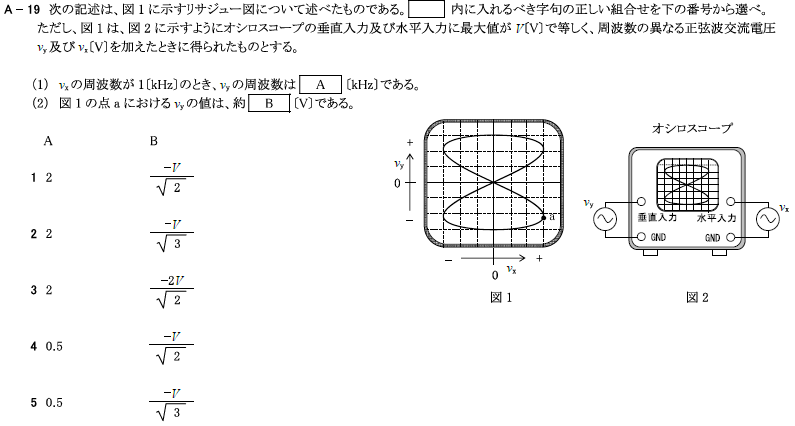
R4.01-2A19
\(4 0.5 \frac{-V}{\sqrt{2}}\)

R6.07-1A19と同じ。
R2.01-1A18
\(3 0.5 \frac{-V}{\sqrt{2}}\)
R3.01-2A20
\(3 600 0 \frac{1}{200}\)

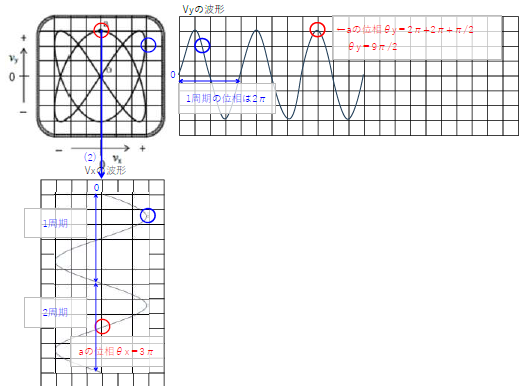
(1)\(V_x\)と\(V_y\)の周波数比をピークの数から求める
X軸方向に増減が変化するピーク数(〇)は4、Y軸方向に増減が変化するピーク数(〇)は6
\(x:y=4:6=2:3 2y=3x y=\frac{3}{2}x\)
\(x=400Hzのとき、y=\frac{3}{2}×400Hz=600Hz\)
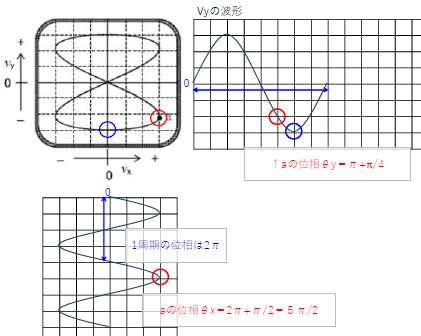
(2)上図の点aから\(V_x\)に垂直に下した矢印(2)より、0V
(3)点oから始まって点oに戻るまでの時間は、\(V_x\)の2周期分となる。
よって求める時間\(T\)は、\(V_x\)の周期を\(T_x\)、波長を\(f_x\)とすると、
\(時間T=2T_x=2×\frac{1}{f_x}=2×\frac{1}{400}=\frac{1}{200}\)[s]
検索用キーワード(問題文の最初の一文)
図1に示すリサジュー図


コメント