R6.01-1A19

R5.01-1A19

R3.07-2A19
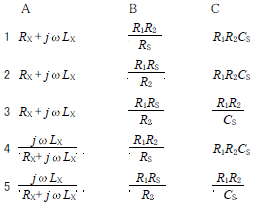
R2.11-2A19
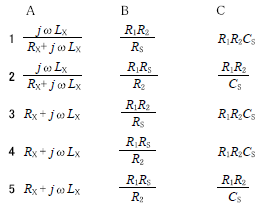
R3.01-2A19

R6.07-1A20

R4.07-2A20

解答
R6.01-1A19
\(5 R_X+jωL_X \frac{R_1R_2}{R_S} R_1R_2C_S\)
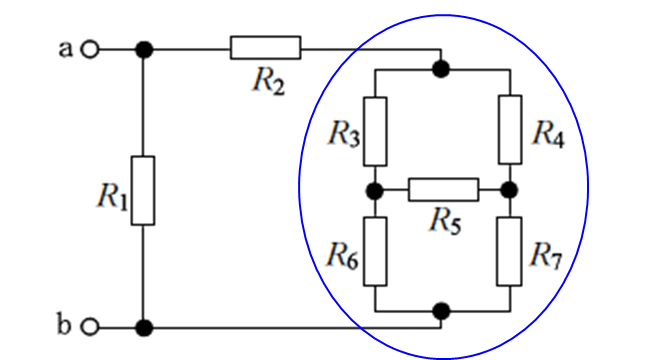
ポイント
この形はブリッジの合成抵抗の問題
対角線の抵抗の積
\(R_3×R_7=R_4×R_6\) ならば
平衡状態で\(R_5\)は無視出来る。

(1)コイル側のインピーダンスAは、
\(A=R_X+jωL_X\)
(2) (1)より、①の式は、
\(R_1R_2=(R_X+jωL_X)×\frac{R_S}{1+jωC_SR_S}\)
分数を整理して、右辺と左辺の実数部と虚数部\((j)\)を比較する
\((1+jωC_SR_S)R_1R_2=(R_X+jωL_X)R_S\)
\(R_1R_2+jωC_SR_SR_1R_2=R_XR_S+jωL_XR_S\)
実数部を比較して
\(R_1R_2=R_XR_S\)
\(R_X=\frac{R_1R_2}{R_S}\)
虚数部を比較して
\(jωC_SR_SR_1R_2=jωL_XR_S\)
\(L_X=\frac{jωC_SR_SR_1R_2}{jωR_S}=C_SR_1R_2\)
R5.01-1A19
\(3 R_X+jωL_X \frac{R_1R_2}{R_S} R_1R_2C_S\)

R3.07-2A19
\(1 R_X+jωL_X \frac{R_1R_2}{R_S} R_1R_2C_S\)
R2.11-2A19
\(3 R_X+jωL_X \frac{R_1R_2}{R_S} R_1R_2C_S\)
R3.01-2A19
\(1 \frac{R_S}{1+jωC_SR_S} \frac{R_1R_2}{R_S} R_1R_2C_S\)

(1)\(C_S\)と\(R_S\)側のインピーダンスAは、
\(A=\frac{R_S×\frac{1}{jωC_S}}{R_S+\frac{1}{jωC_S}}=\frac{R_S}{1+jωC_SR_S}\) 並列の合成は和分の積\(=\frac{積}{和}\)
(2) (1)より、①の式は、
\(R_1R_2=(R_X+jωL_X)×\frac{R_S}{1+jωC_SR_S}\)
分数を整理して、右辺と左辺の実数部と虚数部\((j)\)を比較する
\((1+jωC_SR_S)R_1R_2=(R_X+jωL_X)R_S\)
\(R_1R_2+jωC_SR_SR_1R_2=R_XR_S+jωL_XR_S\)
実数部を比較して
\(R_1R_2=R_XR_S\)
\(R_X=\frac{R_1R_2}{R_S}\)
虚数部を比較して
\(jωC_SR_SR_1R_2=jωL_XR_S\)
\(L_X=\frac{jωC_SR_SR_1R_2}{jωR_S}=C_SR_1R_2\)
R6.07-1A20
\(5 30[Ω] 6×10^{-4}[H]\)

①平衡条件より、
\(R_1R_2=(R_0+jωL)×\frac{R_3×\frac{1}{jωC}}{R_3+\frac{1}{jωC}}\)
② ①の式の分数を整理して、右辺と左辺の実数部と虚数部\((j)\)を比較する
\(R_1R_2=(R_0+jωL)×\frac{R_3}{1+jωCR_3}\)
\((1+jωCR_3)R_1R_2=(R_0+jωL)R_3\)
\(R_1R_2+jωCR_1R_2R_3=R_0R_3+jωLR_3\)
実数部を比較して
\(R_1R_2=R_0R_3\)
\(R_0=\frac{R_1R_2}{R_3}=\frac{100×600}{2k}=\frac{60000}{2000}=30\)[Ω]
虚数部を比較して
\(jωCR_1R_2R_3=jωLR_3\)
\(CR_1R_2=L\)
\(L=CR_1R_2=0.01μ×100×600=0.01×10^{-6}×6×10^{4}=6×10^{-4}\)[H]
R4.07-2A20
\(1 25[Ω] 5×10^{-4}[H]\)

①平衡条件より、
\(R_1R_2=(R_0+jωL)×\frac{R_3×\frac{1}{jωC}}{R_3+\frac{1}{jωC}}\)
② ①の式の分数を整理して、右辺と左辺の実数部と虚数部\((j)\)を比較する
\(R_1R_2=(R_0+jωL)×\frac{R_3}{1+jωCR_3}\)
\((1+jωCR_3)R_1R_2=(R_0+jωL)R_3\)
\(R_1R_2+jωCR_1R_2R_3=R_0R_3+jωLR_3\)
実数部を比較して
\(R_1R_2=R_0R_3\)
\(R_0=\frac{R_1R_2}{R_3}=\frac{100×500}{2k}=\frac{50000}{2000}=25\)[Ω]
虚数部を比較して
\(jωCR_1R_2R_3=jωLR_3\)
\(CR_1R_2=L\)
\(L=CR_1R_2=0.01μ×100×500=0.01×10^{-6}×5×10^{4}=5×10^{-4}\)[H]
検索用キーワード(問題文の最初の一文)
図に示すブリッジ回路を用いてコイルの自己インダクタンス\(L_X[H]\)及び抵抗\(R_X[Ω]\)を求める方法
図に示すブリッジ回路が平衡しているとき、抵抗\(R_0[Ω]\)及びインダクタンス\(L\)の値の組合せ


コメント