R6.07-1A10

R3.07-1A10
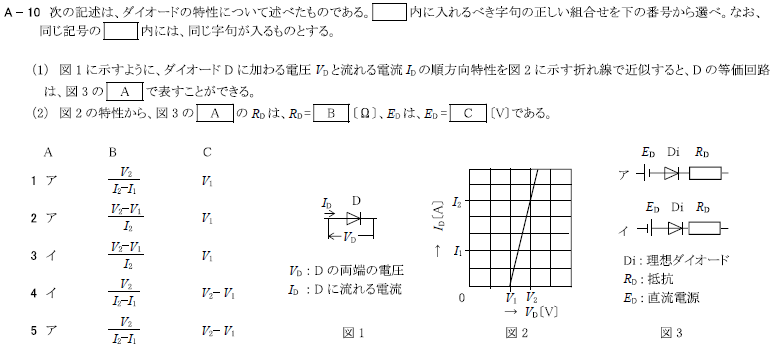
R2.01-1A10
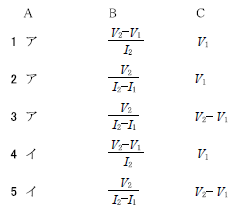
R7.07-1A10
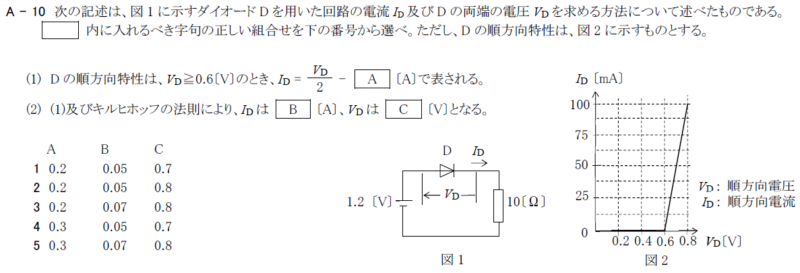
R5.07-1A10
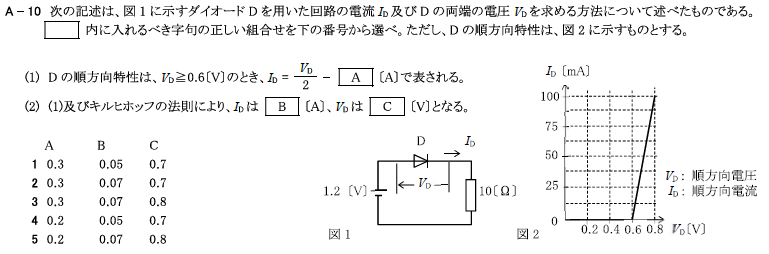
R4.07-2A10
R6.01-1A10
R3.01-1A10
解答
R6.07-1A10
\(3 ア \frac{V_2-V_1}{I_2} V_1\)
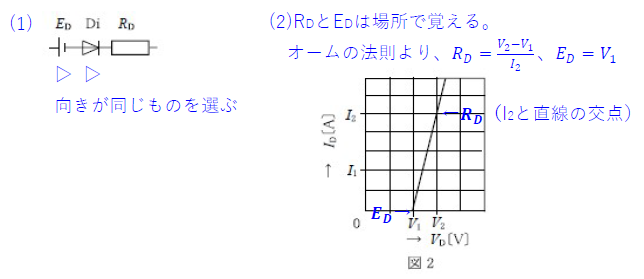
ワンポイント解説

R3.07-1A10
\(2 ア \frac{V_2-V_1}{I_2} V_1\)

R2.01-1A10
\(1 ア \frac{V_2-V_1}{I_2} V_1\)
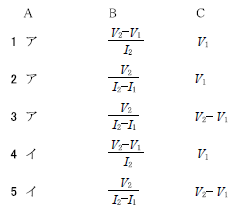
R7.07-1A10
4 0.3 0.05 0.7
ワンポイント解説
(1)\(V_D≧0.6\)の直線の式を書く
(2)ダイオードの等価回路を書く

(1)\(V_D≧0.6\)の直線の式を書く
馴染みがあるように縦軸を\(y\)、横軸を\(x\)とすると、直線の式は、
\(y=ax+b aは傾き、bはy軸との交点\)
\(傾きaは、a=\frac{0.1(=100mV)}{0.8-0.6}=\frac{1}{2}より、\)
\(y=\frac{1}{2}x+b\) -①
この直線は、\((x,y)=(0.6,0)\)を通るので式①に代入して\(b\)を求めます。
\(0=\frac{1}{2}×0.6+b\)
\(b=-0.3\)
したがって、①の式は
\(y=\frac{1}{2}x-0.3\)
最後に縦軸を\(I_D\)、横軸を\(V_D\)に戻すと、直線の式は、
\(I_D=\frac{1}{2}V_D-0.3\)
(2)ダイオードの等価回路を書く
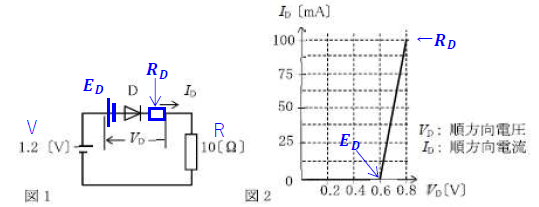
\(I_D=\frac{V-E_D}{R+R_D}\)
\(R_D\)は、図2のグラフより、
\(R_D=\frac{ΔV}{ΔI}=\frac{0.8-0.6}{0.1}=2\)
\(I_D=\frac{1.2-0.6}{10+2}=\frac{0.6}{12}=0.05\)
\(V_D=E_D+R_D×I_D=0.6+2×0.05=0.6+0.1=0.7\)
R5.07-1A10
1 0.3 0.05 0.7

問題と解は同上。
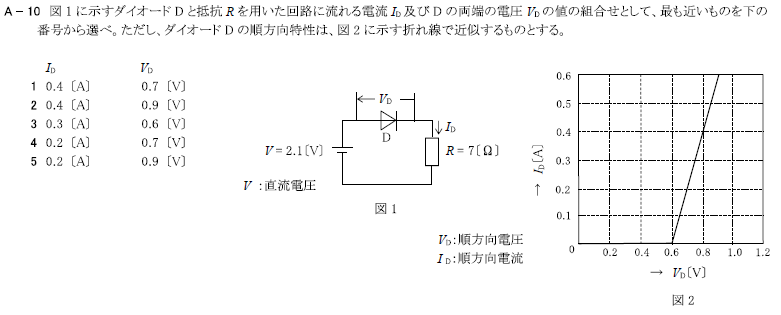
R4.07-2A10
3 0.2[A] 0.6[V]

ダイオードの等価回路を書く
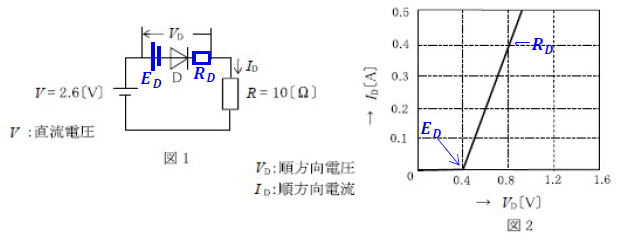
\(I_D=\frac{V-E_D}{R+R_D}\)
\(R_D\)は、図2のグラフより、
\(R_D=\frac{ΔV}{ΔI}=\frac{0.8-0.4}{0.4}=1\)
\(I_D=\frac{2.6-0.4}{10+1}=\frac{2.2}{11}=0.2\)
\(V_D=E_D+R_D×I_D=0.4+1×0.2=0.4+0.2=0.6\)
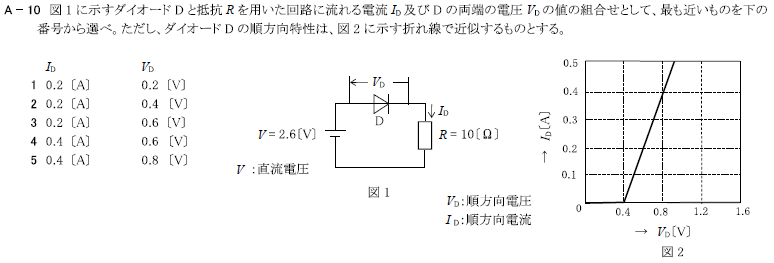
R6.01-1A10
1 0.2[A] 0.7[V]

ダイオードの等価回路を書く
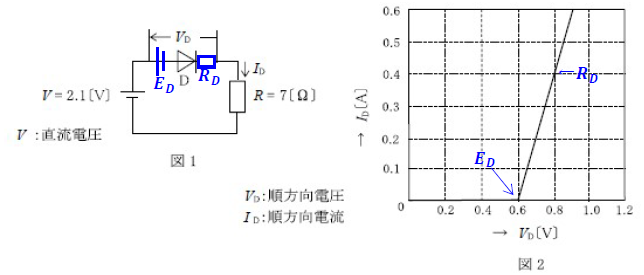
\(I_D=\frac{V-E_D}{R+R_D}\)
\(R_D\)は、図2のグラフより、
\(R_D=\frac{ΔV}{ΔI}=\frac{0.8-0.6}{0.4}=0.5\)
\(I_D=\frac{2.1-0.6}{7+0.5}=\frac{1.5}{7.5}=0.2\)
\(V_D=E_D+R_D×I_D=0.6+0.5×0.2=0.6+0.1=0.7\)
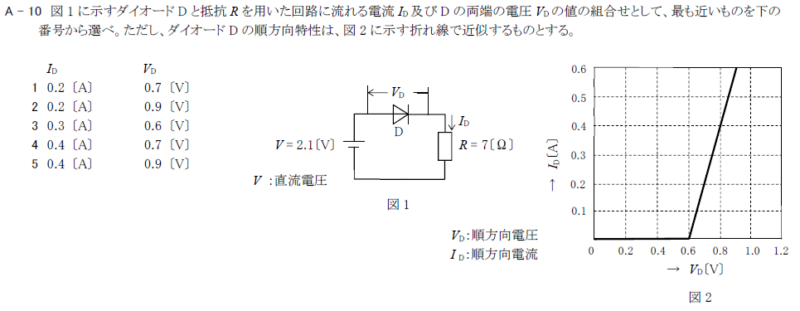
R3.01-1A10
4 0.2[A] 0.7[V]

検索用キーワード(問題文の最初の一文)
ダイオードの特性
図1に示すダイオードDを用いた回路の電流\(I_D\)及びDの両端の電圧\(V_D\)を求める方法
図1に示すダイオードDと抵抗Rを用いた回路に流れる電流\(I_D\)及びDの両端の電圧\(V_D\)の値


コメント