基礎1104(1)

R5.07-2B5

R4.01-2B5

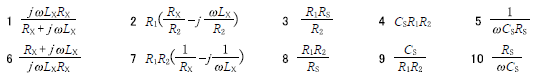
H31.01-1B5

解答へ

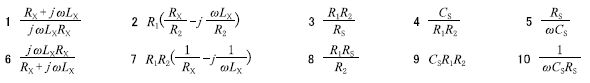
解答

R5.07-2B5

ア　1：\(\frac{R_X+jωL_X}{jωL_XR_X}\)
イ　2：\(R_1R_2(\frac{1}{R_X}-j\frac{1}{ωL_X})\)
ウ　3：\(\frac{R_1R_2}{R_S}\)
エ　9：\(C_sR_1R_2\)
オ　10：\(\frac{1}{ωC_sR_S}\)

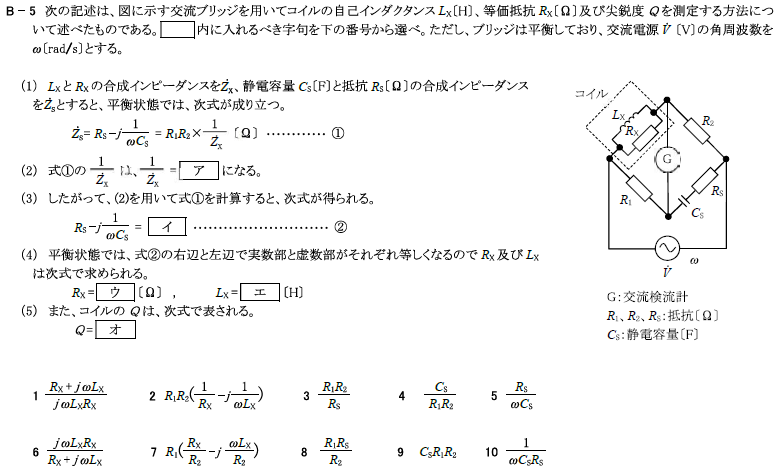
(1)の問題文より、点線のコイル内のインピーダンスが\(\dot{Z}_x\)、
　右下の\(R_s\)と\(C_s\)のインピーダンスを\(\dot{Z}_s\)とすると
　平衡条件より、
　\(\dot{Z}_x\dot{Z}_s=R_1R_2\)
　\(\dot{Z}_s=\frac{R_1R_2}{\dot{Z}_x}=R_s+\frac{1}{jωC_s}=R_s-j\frac{1}{ωC_s}\)　－①

(2)点線内のインピーダンス\(\dot{Z}_x\)は、抵抗とコイルの並列接続より、
　\(\dot{Z}_x=\frac{jωL_xR_x}{R_x+jωL_x}\)
　\(\frac{1}{\dot{Z}_x}=\frac{R_x+jωL_x}{jωL_xR_x}\)　－ア

(3)(2)より、①の式は、
　\(R_s-j\frac{1}{ωC_s}=\frac{R_1R_2}{\dot{Z}_x}=R_1R_2(\frac{R_x+jωL_x}{jωL_xR_x})=R_1R_2(\frac{1}{R_x}+\frac{1}{jωL_x})=R_1R_2(\frac{1}{R_x}-j\frac{1}{ωL_x})\))　－②

(4)②の式の
実数部　\(R_s=\frac{R_1R_2}{R_x}\)
　　　　\(R_x=\frac{R_1R_2}{R_s}\)　－ウ
虚数部　\(-j\frac{1}{ωC_s}=-j\frac{R_1R_2}{ωL_x}\)
　　　　\(\frac{1}{ωC_s}=\frac{R_1R_2}{ωL_x}\)
　　　　\(L_x=C_sR_1R_2\)　－エ

(5)・直列回路の尖鋭度\(Q=\frac{ωL}{R}\)
　・並列回路の尖鋭度\(Q=\frac{R}{ωL}\)より、
点線内のコイルの先鋭度\(Q\)は、並列接続だから
　尖鋭度\(Q=\frac{R}{ωL}=\frac{1}{ω}×\frac{R_1R_2}{R_s}×\frac{1}{C_sR_1R_2}=\frac{1}{ωC_sR_s}\)

R4.01-2B5

ア　6：\(\frac{R_X+jωL_X}{jωL_XR_X}\)
イ　7：\(R_1R_2(\frac{1}{R_X}-j\frac{1}{ωL_X})\)
ウ　8：\(\frac{R_1R_2}{R_S}\)
エ　4：\(C_sR_1R_2\)
オ　5：\(\frac{1}{ωC_sR_S}\)

H31.01-1B5

ア　1：\(\frac{R_X+jωL_X}{jωL_XR_X}\)
イ　7：\(R_1R_2(\frac{1}{R_X}-j\frac{1}{ωL_X})\)
ウ　3：\(\frac{R_1R_2}{R_S}\)
エ　9：\(C_sR_1R_2\)
オ　10：\(\frac{1}{ωC_sR_S}\)

前の問題へ

次の問題へ