R8.01-1B2
R5.07-2B2
R7.07-1B2
R5.01-2B2
R4.07-1A7
R3.01-2A8
R6.07-1B2
R4.01-1B2
R2.11-2B2
R3.07-2A7
R2.01-1A7
R1.07-1A8
解答
R8.01-1B2
ア：１ 四端子定数
イ：２ 1+j2
ウ：８ j60［Ω］
エ：９ \(\frac{1}{30}\)［S］
オ：５ 1
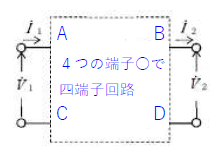
ワンポイント解説
四端子回路
①出力オープン（\(I_2=0\)）の時
\(\dot{A}=\frac{\dot{V}_1}{\dot{V}_2} \dot{C}=\frac{\dot{I}_1}{\dot{V}_2}\)
②出力ショート（\(V_2=0\)）の時
\(\dot{B}=\frac{\dot{V}_1}{\dot{I}_2} \dot{D}=\frac{\dot{I}_1}{\dot{I}_2}\)
①出力オープン（\(I_2=0\)）の時、\(I_1\)は下図の様になる。
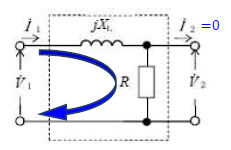
\(\dot{A}=\frac{\dot{V}_1}{\dot{V}_2}=\frac{(jX_L+R)I_1}{RI_1}=\frac{jX_L+R}{R}=\frac{j60+30}{30}=1+j2\)
\(\dot{C}=\frac{\dot{I}_1}{\dot{V}_2}=\frac{I_1}{RI_1}=\frac{I_1}{30I_1}=\frac{1}{30}\)
②出力ショート（\(V_2=0\)）の時、\(I_1\)は下図の様になる。
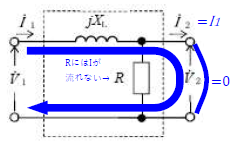
\(\dot{B}=\frac{\dot{V}_1}{\dot{I}_2}=\frac{jX_LI_1}{I_1}=jX_L=j60\)
\(\dot{D}=\frac{\dot{I}_1}{\dot{I}_2}=\frac{I_1}{I_1}=1\)
R5.07-2B2
ア：６ 四端子定数
イ：７ 1+j2
ウ：３ j60［Ω］
エ：９ \(\frac{1}{30}\)［S］
オ：１０ 1
問題と解は同上。
R7.07-1B2
ア：１ 四端子定数
イ：２ \(\frac{R_1+R_3}{R_3}\)
ウ：８ 500
エ：４ \(\frac{1}{400}\)
オ：５ \(\frac{3}{2}\)
①出力オープン（\(I_2=0\)）の時、\(I_1\)は\(R_1→R_3\)に流れるから、
\(\dot{A}=\frac{\dot{V}_1}{\dot{V}_2}=\frac{(R_1+R_3)I_1}{R_3I_1}=\frac{R_1+R_3}{R_3}\)
\(\dot{C}=\frac{\dot{I}_1}{\dot{V}_2}=\frac{I_1}{R_3I_1}=\frac{1}{400}\)
②出力ショート（\(V_2=0\)）の時、\(R_2\)と\(R_3\)は並列接続となるから、
\(\dot{B}=\frac{\dot{V}_1}{\dot{I}_2}=\frac{I_1(R_1+\frac{R_2R_3}{R_2+R_3})}{I_1×\frac{R_3}{R_2+R_3}}=\frac{R_1R_2+R_1R_3+R_2R_3}{R_3}\)
\(=\frac{R_1R_2}{R_3}+R_1+R_2=\frac{200×200}{400}+200+200=500\)
\(\dot{D}=\frac{\dot{I}_1}{\dot{I}_2}=\frac{I_1}{I_1×\frac{R_3}{R_2+R_3}}=\frac{R_2+R_3}{R_3}=\frac{600}{400}=\frac{3}{2}\)
R5.01-2B2
ア：６ 四端子定数
イ：７ \(\frac{R_1+R_3}{R_3}\)
ウ：３ 500
エ：９ \(\frac{1}{400}\)
オ：１０ \(\frac{3}{2}\)
問題と解は同上。
R4.07-1A7
２ \(1+j2 j40［Ω］ \frac{1}{20}［S］ 1\)
①出力オープン（\(I_2=0\)）の時、\(I_1\)は\(jX_L→R\)に流れるから、
\(\dot{A}=\frac{\dot{V}_1}{\dot{V}_2}=\frac{(jX_L+R)I_1}{RI_1}=\frac{jX_L+R}{R}=\frac{j40+20}{20}=1+j2\)
\(\dot{C}=\frac{\dot{I}_1}{\dot{V}_2}=\frac{I_1}{RI_1}=\frac{I_1}{20I_1}=\frac{1}{20}\)
②出力ショート（\(V_2=0\)）の時、\(I_1\)は\(R\)には流れないから、
\(\dot{B}=\frac{\dot{V}_1}{\dot{I}_2}=\frac{jX_LI_1}{I_1}=jX_L=j40\)
\(\dot{D}=\frac{\dot{I}_1}{\dot{I}_2}=\frac{I_1}{I_1}=1\)
R3.01-2A8
２ \(1+j2 j60［Ω］ \frac{1}{30}［S］ 1\)
①出力オープン（\(I_2=0\)）の時、\(I_1\)は\(jX_L→R\)に流れるから、
\(\dot{A}=\frac{\dot{V}_1}{\dot{V}_2}=\frac{(jX_L+R)I_1}{RI_1}=\frac{jX_L+R}{R}=\frac{j60+30}{30}=1+j2\)
\(\dot{C}=\frac{\dot{I}_1}{\dot{V}_2}=\frac{I_1}{RI_1}=\frac{I_1}{30I_1}=\frac{1}{30}\)
②出力ショート（\(V_2=0\)）の時、\(I_1\)は\(R\)には流れないから、
\(\dot{B}=\frac{\dot{V}_1}{\dot{I}_2}=\frac{jX_LI_1}{I_1}=jX_L=j60\)
\(\dot{D}=\frac{\dot{I}_1}{\dot{I}_2}=\frac{I_1}{I_1}=1\)
R6.07-1B2
ア：６ 四端子定数
イ：７ 1－j3
ウ：３ －j90［Ω］
エ：９ \(\frac{1}{30}\)［S］
オ：５ 1
①出力オープン（\(I_2=0\)）の時、\(I_1\)は\(jX_C→R\)に流れるから、
\(\dot{A}=\frac{\dot{V}_1}{\dot{V}_2}=\frac{(-jX_C+R)I_1}{RI_1}=\frac{-jX_C+R}{R}=\frac{-j90+30}{30}=1-j3\)
\(\dot{C}=\frac{\dot{I}_1}{\dot{V}_2}=\frac{I_1}{RI_1}=\frac{I_1}{30I_1}=\frac{1}{30}\)
②出力ショート（\(V_2=0\)）の時、\(I_1\)は\(R\)には流れないから、
\(\dot{B}=\frac{\dot{V}_1}{\dot{I}_2}=\frac{jX_CI_1}{I_1}=jX_C=-j90\)
\(\dot{D}=\frac{\dot{I}_1}{\dot{I}_2}=\frac{I_1}{I_1}=1\)
R4.01-1B2
ア：１ 四端子定数
イ：２ 1－j3
ウ：８ －j90［Ω］
エ：４ \(\frac{1}{30}\)［S］
オ：５ 1
解き方は、R6.07-1B2と同じ。
R2.11-2B2
ア：６ 四端子定数
イ：２ 1－j3
ウ：３ －j90［Ω］
エ：４ \(\frac{1}{30}\)［S］
オ：１０ 1
R3.07-2A7
１ \(\frac{3}{2} 500［Ω］ \frac{1}{400}［S］ \frac{3}{2}\)
①出力オープン（\(I_2=0\)）の時、\(I_1\)は\(R_1→R_3\)に流れるから、
\(\dot{A}=\frac{\dot{V}_1}{\dot{V}_2}=\frac{(R_1+R_3)I_1}{R_3I_1}=\frac{R_1+R_3}{R_3}=\frac{200+400}{400}=\frac{3}{2}\)
\(\dot{C}=\frac{\dot{I}_1}{\dot{V}_2}=\frac{I_1}{R_3I_1}=\frac{1}{400}\)
②出力ショート（\(V_2=0\)）の時、\(R_2\)と\(R_3\)は並列接続となるから、
\(\dot{B}=\frac{\dot{V}_1}{\dot{I}_2}=\frac{I_1(R_1+\frac{R_2R_3}{R_2+R_3})}{I_1×\frac{R_3}{R_2+R_3}}=\frac{R_1R_2+R_1R_3+R_2R_3}{R_3}\)
\(=\frac{R_1R_2}{R_3}+R_1+R_2=\frac{200×200}{400}+200+200=500\)
\(\dot{D}=\frac{\dot{I}_1}{\dot{I}_2}=\frac{I_1}{I_1×\frac{R_3}{R_2+R_3}}=\frac{R_2+R_3}{R_3}=\frac{600}{400}=\frac{3}{2}\)
R2.01-1A7
３ \(2 300［Ω］ \frac{1}{100}［S］ 2\)
①出力オープン（\(I_2=0\)）の時、\(I_1\)は\(R_1→R_3\)に流れるから、
\(\dot{A}=\frac{\dot{V}_1}{\dot{V}_2}=\frac{(R_1+R_3)I_1}{R_3I_1}=\frac{R_1+R_3}{R_3}=\frac{100+100}{100}=2\)
\(\dot{C}=\frac{\dot{I}_1}{\dot{V}_2}=\frac{I_1}{R_3I_1}=\frac{1}{100}\)
②出力ショート（\(V_2=0\)）の時、\(R_2\)と\(R_3\)は並列接続となるから、
\(\dot{B}=\frac{\dot{V}_1}{\dot{I}_2}=\frac{I_1(R_1+\frac{R_2R_3}{R_2+R_3})}{I_1×\frac{R_3}{R_2+R_3}}=\frac{R_1R_2+R_1R_3+R_2R_3}{R_3}\)
\(=\frac{R_1R_2}{R_3}+R_1+R_2=\frac{100×100}{100}+100+100=300\)
\(\dot{D}=\frac{\dot{I}_1}{\dot{I}_2}=\frac{I_1}{I_1×\frac{R_3}{R_2+R_3}}=\frac{R_2+R_3}{R_3}=\frac{200}{100}=2\)
R1.07-1A8
４ \(1+j2 j60［Ω］ \frac{1}{30}［S］ 1\)
①出力オープン（\(I_2=0\)）の時、\(I_1\)は\(jX_L→R\)に流れるから、
\(\dot{A}=\frac{\dot{V}_1}{\dot{V}_2}=\frac{(jX_L+R)I_1}{RI_1}=\frac{jX_L+R}{R}=\frac{j60+30}{30}=1+j2\)
\(\dot{C}=\frac{\dot{I}_1}{\dot{V}_2}=\frac{I_1}{RI_1}=\frac{I_1}{30I_1}=\frac{1}{30}\)
②出力ショート（\(V_2=0\)）の時、\(I_1\)は\(R\)には流れないから、
\(\dot{B}=\frac{\dot{V}_1}{\dot{I}_2}=\frac{jX_LI_1}{I_1}=jX_L=j60\)
\(\dot{D}=\frac{\dot{I}_1}{\dot{I}_2}=\frac{I_1}{I_1}=1\)
検索用キーワード（問題文の最初の一文）
図に示す回路とその定数
図に示す四端子回路網において、各定数（\(\dot{A}\)、\(\dot{B}\)、\(\dot{C}\)、\(\dot{D}\)）の値の組合せ
コメント