基礎806

R6.01-1A16

解答

R6.01-1A16

２

ワンポイント解説

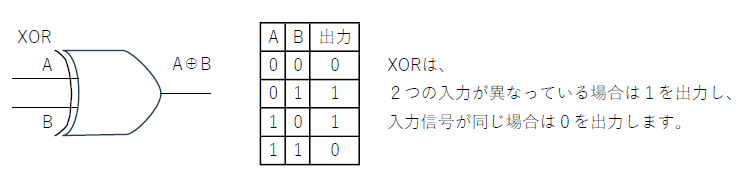
①\(入力が(A2,A1)=(0,0)、(B2,B1)=(0,0)の時は、\)
　１　\(F=(A1⊕B1)⊕(A2⊕B2)=0⊕0=0\)
　　　\((A2,A1)\)と\((B2,B1)\)が一致しない場合のみ、出力\(F\)を1としたいので、OK
　２　\(F=(A1⊕B1)+(A2⊕B2)=0+0=0\)　OK
　３　\(F=\overline{(A1⊕B1)×(A2⊕B2)}=\overline{0×0}=1\)　NG
　４　\(F=(A1⊕B1)×(A2⊕B2)=0×0=0\)　OK
　５　\(F=\overline{(A1⊕B1)+(A2⊕B2)}=\overline{0+0}=1\)　NG

②\(入力が(A2,A1)=(0,1)、(B2,B1)=(0,0)の時は、\)
　１　\(F=(A1⊕B1)⊕(A2⊕B2)=(1⊕0)⊕(0⊕0)=1⊕0=1\)
　　　\((A2,A1)\)と\((B2,B1)\)が一致しない場合のみ、出力\(F\)を1としたいので、OK
　２　\(F=(A1⊕B1)+(A2⊕B2)=1+0=1\)　OK
　４　\(F=(A1⊕B1)×(A2⊕B2)=1×0=0\)　NG

③\(入力が(A2,A1)=(0,1)、(B2,B1)=(1,0)の時は、\)
　１　\(F=(A1⊕B1)⊕(A2⊕B2)=(1⊕0)⊕(0⊕1)=1⊕1=0\)
　　　\((A2,A1)\)と\((B2,B1)\)が一致しない場合のみ、出力\(F\)を1としたいので、NG
　２　\(F=(A1⊕B1)+(A2⊕B2)=1+1=1\)　OK

検索用キーワード（問題文の最初の一文）

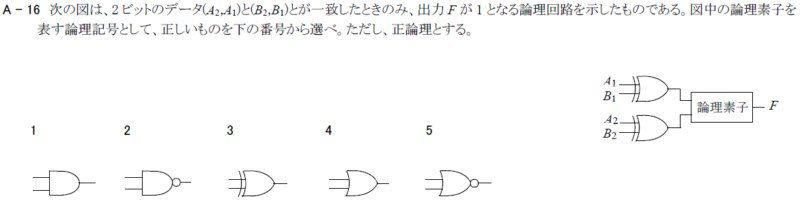
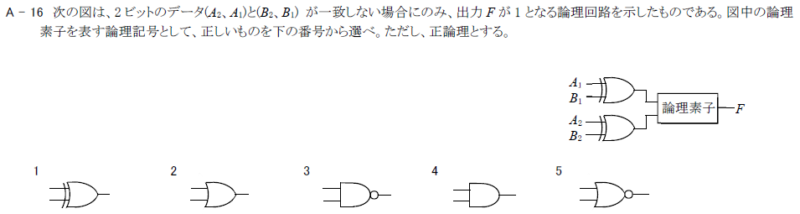
次の図は、2ビットのデータ(A2,A1)と(B2,B1)が一致しない場合にのみ、出力Fが1となる論理回路を示したものである。図中の論理回路素子を表す論理記号