BR8.01出題予想
R4.01-2B5

R3.01-1B5
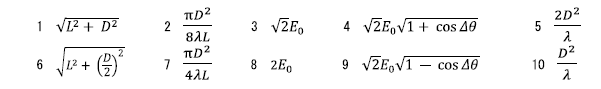
H31.01-1B5
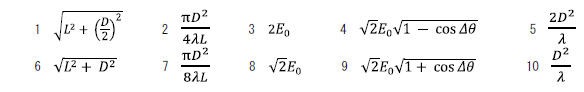
解答
R4.01-2B5
ア 6 \(\sqrt{L^2+(\frac{D}{2})^2}\)
イ 2 \(\frac{πD^2}{4λL}\)
ウ 8 \(2E_0\)
エ 9 \(\sqrt{2}E_0\sqrt{1+\cos{Δθ}}\)
オ 10 \(\frac{2D^2}{λ}\)
ワンポイント解説 語呂合わせ 語呂合わせ
アンテナ利得(ビッグサイズ)の測定距離
\(\sqrt{L^2+(\frac{D}{2})^2}\) ドームを2つに割ると(\(\frac{D}{2}\))
\(\frac{πD^2}{4λL}\) ドジョウが4匹(\(\frac{D^2}{4}\))
\(2E_0\) イーゼロ2倍と(\(2E_0\))
\(\sqrt{2}E_0\sqrt{1+\cos{Δθ}}\) コサイン足して(\(1+\cos{}\))
\(\frac{2D^2}{λ}\) ツーデーツー(\(2D^2\))

R3.01-1B5
ア 6 \(\sqrt{L^2+(\frac{D}{2})^2}\)
イ 7 \(\frac{πD^2}{4λL}\)
ウ 8 \(2E_0\)
エ 4 \(\sqrt{2}E_0\sqrt{1+\cos{Δθ}}\)
オ 5 \(\frac{2D^2}{λ}\)
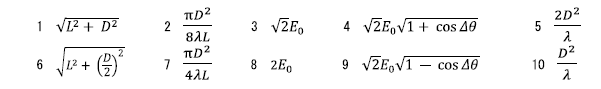
H31.01-1B5
ア 1 \(\sqrt{L^2+(\frac{D}{2})^2}\)
イ 2 \(\frac{πD^2}{4λL}\)
ウ 3 \(2E_0\)
エ 9 \(\sqrt{2}E_0\sqrt{1+\cos{Δθ}}\)
オ 5 \(\frac{2D^2}{λ}\)
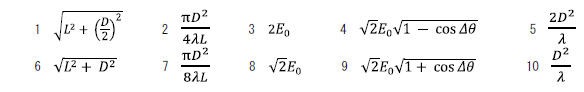
検索用キーワード(問題文の最初の一文)
アンテナ利得などの測定において、送信又は受信アンテナの一方の開口の大きさが波長に比べて大きいときの測定距離


コメント