R7.07-1A4
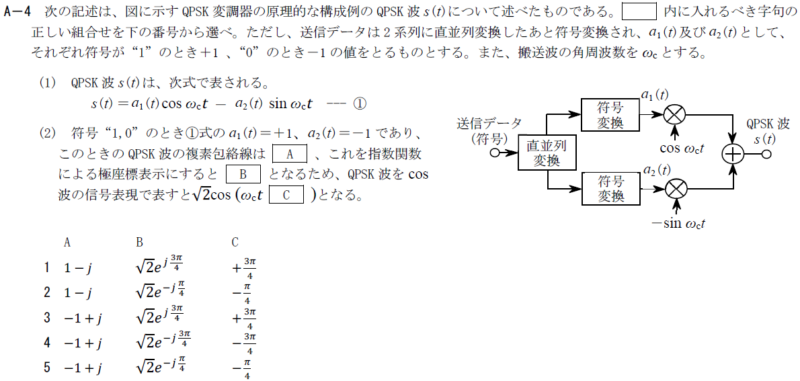
R3.07-1A2

R2.11-2A2
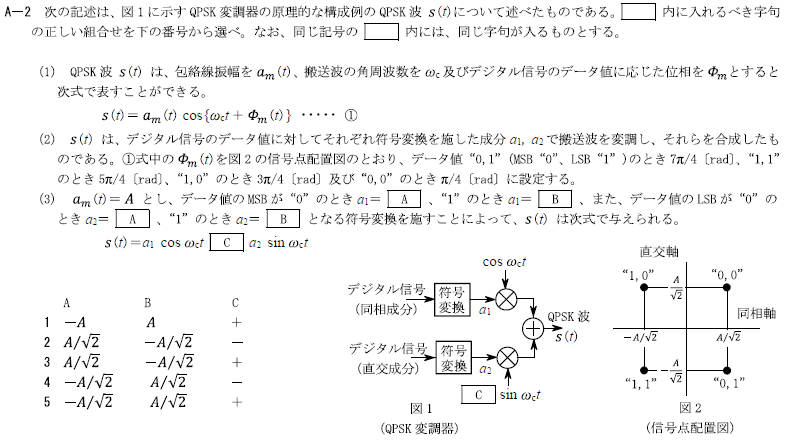
R2.11-1A2
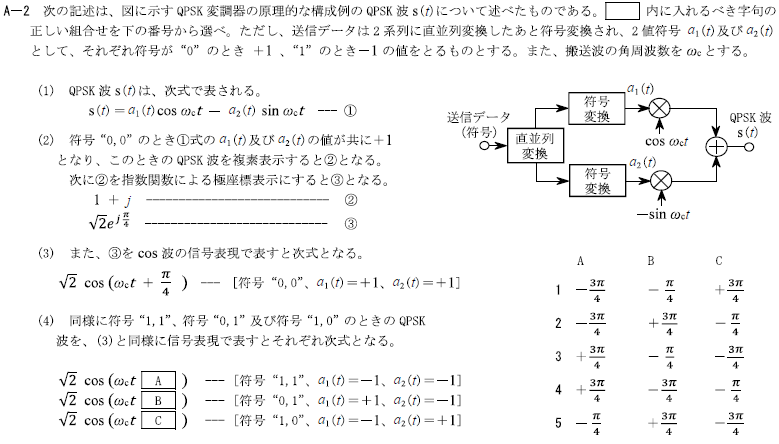
解答
R7.07-1A4
2 \(1-j \sqrt{2}e^{-j\frac{π}{4}} -\frac{π}{4}\)
ワンポイント解説
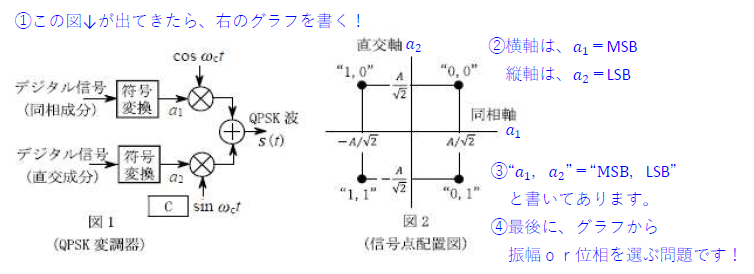

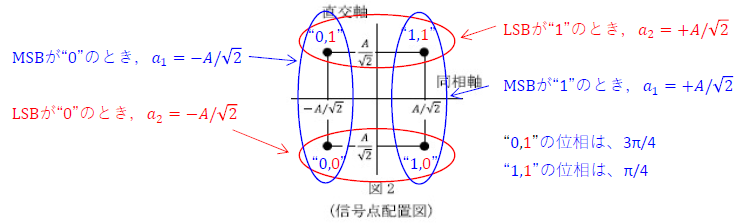
(2) 符号“1,0”のときは、上図の右下ですので、
複素包絡線で表すと、\(1-j\) -A
指数関数による極座標表示にすると、eの自乗は位相となるので\(-j\frac{π}{4}\) -B
\(\cos\)波の信号表現で表すと位相は\(-\frac{π}{4}\) -C
R3.07-1A2
1 3π/4 π/4


R2.11-2A2
2 \(A/\sqrt{2} -A/\sqrt{2} -\)

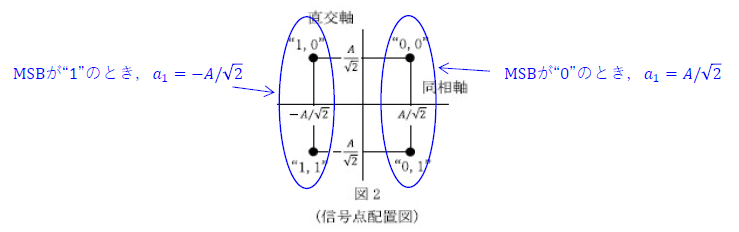
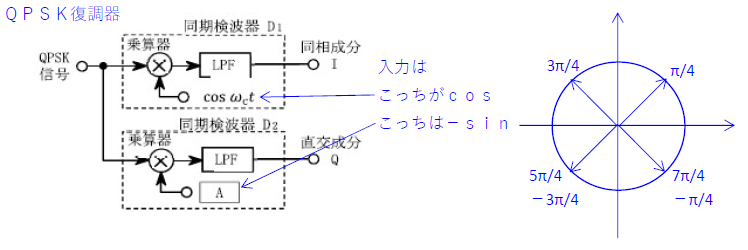
R2.11-1A2
1 \(-\frac{3π}{4} -\frac{π}{4} +\frac{3π}{4}\)

(3)と(4)の[ ]内をグラフに書くと下記になる。
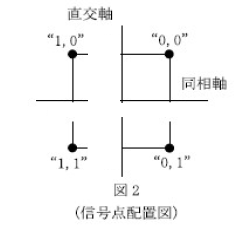
“1,1”の位相は\(-\frac{3π}{4}\) -A
“0,1”の位相は\(-\frac{π}{4}\) -B
“1,0”の位相は\(\frac{3π}{4}\) -C
検索用キーワード(問題文の最初の一文)
・図に示すQPSK変調器の原理的な構成例のQPSK波s(t)
・図1に示すQPSK変調器の原理的な構成例のQPSK波s(t)


コメント