R6.07-1A17

R4.07-1A13

解答
R6.07-1A17
5 59.3[dBm] 42.5[dBμV/m]
ワンポイント解説
①送信機出力電力を[W]→[dBm]にデシベル計算
②EIRPを計算
※EIRPとは、送信機出力から給電線損失、アンテナ利得など送信アンテナの放射器から電波として発射された直後(伝搬距離が未だ無い位に直後)の電力値[dBm]の事です。
③PFDを与えられた式の通りに計算

①送信機出力電力を[W]→[dBW]にデシベル計算(素因数分解)
真数[W]:120=2×2×3×10
[dBW]: =3+3+4.8+10=20.8[dBW]
※log103=0.48は、真数3倍は+4.8dBと言う事を教えてくれています。
デシベル計算(素因数分解) ※電圧は2倍
+10dB=10倍 +3dB=2倍
-10dB=1/10倍 -3dB=1/2倍
✕は+、÷は-
②EIRPを計算
送信機出力 20.8[dBW]
送信アンテナ利得 41[dBi]
給電線損失 2[dB]
ポインティング損失 0.5[dB]
より、EIRP=20.8+41-2-0.5=59.3[dBW]
③伝搬距離を考慮してPFDを計算
問題文より、\(PFD=E^2/(120π)=EIRP/(4πd^2)\)[W/㎡] ←EIRPは[dB]、その他は真数、、、
③-1 \(E^2\)を求めつつ、\(E\)を求める。
↑いきなり\(E\)だと√が出てきてデシベル計算出来ません。
\(E^2=\frac{EIRP}{4πd^2}×120π=\frac{30EIRP}{d^2}\)
デシベル計算(素因数分解)すると
真数:\(E^2[V/m]=\frac{30EIRP}{d^2}=\frac{3×10×EIRP}{d×d}\)
[dB]:\(E+E[dBV/m]=4.8+10+EIRP-d-d\)
\(2E=4.8+10+59.3-75.8-75.8=-77.5\)
\(E=-38.75[dBV/m]\) ※デシベル計算 電圧は2倍なので
\(E=-77.5[dBV/m]\)
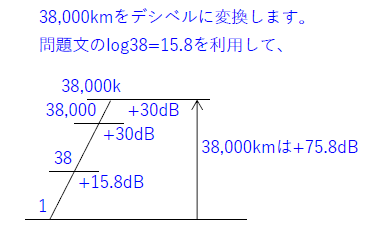
ポイント①\(d=38,000k[m]=75.8[dBm]\)
デシベル計算(素因数分解)
真数[m]:38,000k=38×10×10×10×10×10×10
[dBm]: =15.8+10+10+10+10+10+10=75.8
※log1038=1.58は、真数38倍は+15.8dBと言う事を教えてくれています。
ポイント②デシベル計算 電圧は2倍
計算式最後の電界強度\(E=-38.75[dBV/m]\)は単位が[V]の電圧なので、2倍が必要です。
③-2 \(E=-77.5[dBV/m]\)が求めたが、求める答えの単位は\([dBμV/m]\)。
\(E=1[V/m]=10^6[μV/m]\)(真数)なので
デシベル計算(素因数分解)
真数:\(1[V/m]=10^6[μV/m]=10×10×10×10×10×10[μV/m]\)
[dB]:\(1[dBV/m]=10+10+10+10+10+10[dBμV/m]\)
\( =60[dBμV/m]\) ※デシベル計算 電圧は2倍なので
\( =120[dBμV/m]\)
\(E=1[dBV/m]\)を\([dBμV/m]\)にするには120倍すれば良いので、
求める答えは、
\(E=-77.5[dBV/m]=-77.5+120=42.5[dBμV/m]\)
R4.07-1A13
2 89.3[dBm] -73.3[dBm/㎡]

①送信機出力電力を[W]→[dBm]にデシベル計算
120[W]は2倍と10倍で上手くたどり着く事が出来ないので、問題文のlog103=0.48を利用します。
なぜならば、3倍が使いたい!
log102=0.30の2と0.30は、真数2倍は+3dBの事です。
log1010=1で大きい方の10と1は、真数10倍は+10dBの事です。
=の右側は1/10で記載されています。
よって、3倍は、
log103=0.48は、真数3倍は+4.8dBと言う事を教えてくれています。
と言う事で、送信機出力電力を120[W]→[dBm]にデシベル計算します。
デシベル計算
+10dB=10倍 +3dB=2倍 +4.8dB=3倍
-10dB=1/10倍 -3dB=1/2倍
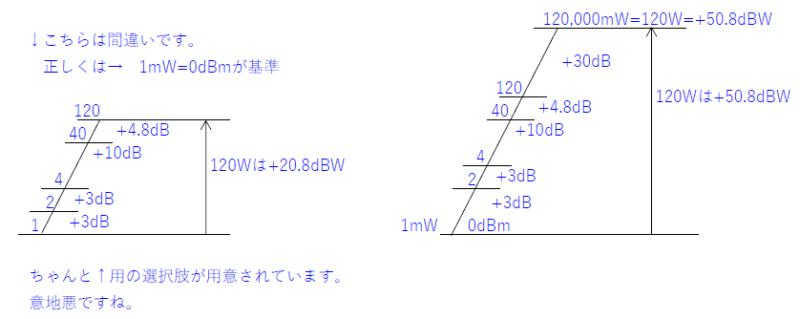
正しくは、0[dBm]=1[mW]が基準になります。
②EIRPを計算
送信機出力 50.8[dBW]
送信アンテナ利得 41[dBi]
給電線損失 2[dB]
ポインティング損失 0.5[dB]
より、EIRP=50.8+41-2-0.5=89.3[dBm]
③伝搬距離を考慮してPFDを計算
問題文より、\(PFD=EIRP/(4πd^2)\)[W/㎡] ←真数の世界
これをデシベルの世界に変換(掛け算→足し算、割り算→引き算)すると
\(PFD=EIRP-4-π-d^2\) ※数字と文字もデシベルに変換すると
\(PFD=89.3[dB]-6[dB]-5[dB]-(38,000k)^2\)
πは問題文(log10π=0.5)、\((38,000k)^2\)はちょっと待った!
2乗は掛け算なので、デシベルの世界に変換すると、
\(PFD=89.3[dB]-6[dB]-5[dB]-38,000k-38,000k)\)
\(PFD=89.3[dB]-6[dB]-5[dB]-75.8[dB]-75.8[dB]=-73.3[dBm]\)
検索用キーワード(問題文の最初の一文)
・放送衛星において、送信機出力電力を120〔W〕、送信アンテナの絶対利得を41〔dBi〕、送信機とアンテナ間の給電線損失(分配器等の挿入損失を含む)を2〔dB〕、アンテナのポインティング損失を0.5〔dB〕、衛星と受信点の距離dを38,000〔km〕とする場合の、衛星の等価等方輻射電力EIRP〔dBW〕及び受信点における電界強度E〔dBμV/m〕の値の組み合わせ
・放送衛星において、送信機出力電力を120[W]、送信アンテナの絶対利得を41[dBi]、送信機とアンテナ間の給電線損失(分配器等の挿入損失を含む)の2[dB]、アンテナのポインティング損失を0.5[dB]、衛星と受信点の距離dを38,000[km]とする場合の、衛星の等価等方輻射電力EIRP[dBm]及び受信点における単位面積当たりの電力束密度PFD[dBm/㎡]の値の組み合わせ


コメント