R6.01-1A19

R4.07-1A18

解答
R6.01-1A19
1 100[m]
ワンポイント解説
最小測定距離\(R_{min}\)は与えられた式\(R_{min}=\frac{2D^2}{λ}\)を利用します。
波長\(λ\)は、\(fλ=c\)より
開口直径\(D\)は、パラボラアンテナ利得\(G=η(\frac{πD}{λ})^2\)から求める。
\(η\):開口効率、\(D\):開口直径

波長\(λ\)は、\(fλ=c\)より
\(λ=\frac{c}{f}=\frac{300M}{30G}=\frac{300M}{30,000M}=0.01\)[m]
開口直径\(D\)は、パラボラアンテナ利得\(G=η(\frac{πD}{λ})^2\)から求める。
\(G=η(\frac{πD}{λ})^2\)
\((\frac{πD}{λ})^2=\frac{G}{η}\)
\(D^2=\frac{G}{η}×\frac{λ^2}{π^2}\) ※\(G\)は真数で代入!
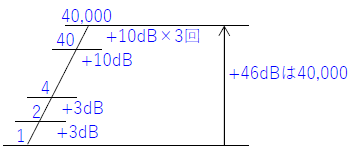
\(D^2=\frac{40,000}{0.8}×\frac{0.01^2}{10}=50\) ※\(π^2≒10\)は覚えておいてください!
最小測定距離\(R_{min}\)は、
\(R_{min}=\frac{2D^2}{λ}=\frac{2×50}{0.01}=100\)[m]
R4.07-1A18
5 200[m]

波長\(λ\)は、\(fλ=c\)より
\(λ=\frac{c}{f}=\frac{300M}{20G}=\frac{300M}{20,000M}=0.015\)[m]
開口直径\(D\)は、パラボラアンテナ利得\(G=η(\frac{πD}{λ})^2\)から求める。
\(G=η(\frac{πD}{λ})^2\)
\((\frac{πD}{λ})^2=\frac{G}{η}\)
\(D^2=\frac{G}{η}×\frac{λ^2}{π^2}\) ※\(G\)は真数で代入!

\(D^2=\frac{40,000}{0.6}×\frac{0.015^2}{10}=1.5\) ※\(π^2≒10\)は覚えておいてください!
最小測定距離\(R_{min}\)は、
\(R_{min}=\frac{2D^2}{λ}=\frac{2×1.5}{0.015}=200\)[m]
検索用キーワード(問題文の最初の一文)
周波数30[GHz]、絶対利得46[dB]、開口能率0.8のパラボラアンテナの指向性を測定するために必要な最小測定距離Rminの値
周波数20[GHz]、絶対利得46[dB]、開口能率60[%]のパラボラアンテナの指向性を測定するために必要な最小測定距離Rminの値


コメント