R6.07-1A17
R4.07-1A14
R3.01-1A17 穴埋め
解答
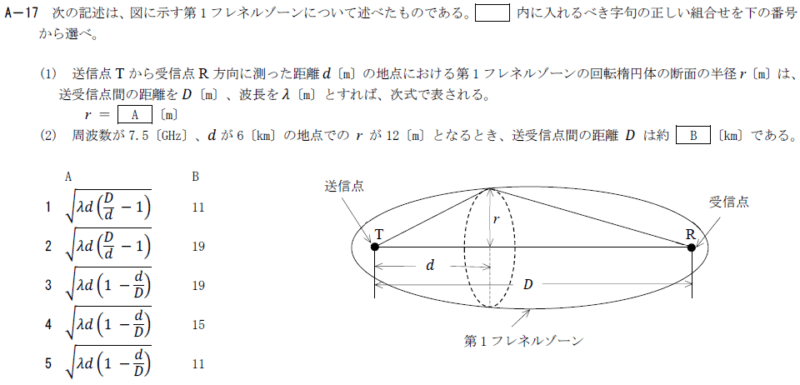
R6.07-1A17
4 \(\sqrt{λd(1-\frac{d}{D})} 15\)
ワンポイント解説 語呂合わせ
第1フレネルゾーンは、第一(1、-1ではない)フレネルゾーン
第1フレネルゾーンの半径\(r\)は、\(r=5\sqrt{\frac{3D}{f}}\)[m]
\(D\):送受信点間の距離[km]、\(f\):周波数[GHz] ※単位に注意
語呂合わせ 5ルート(\(5\sqrt{ }\))のうち、3度(\(3D\)) 復活する(\(f\))

第1フレネルゾーンの半径\(r\)は、\(r=5\sqrt{\frac{3D}{f}}\)[m]
\(r^2=5^2×\frac{3D}{f}\)
\(D=\frac{r^2f}{75}=\frac{12^2×7.5}{75}=14.4≒15\)[km]
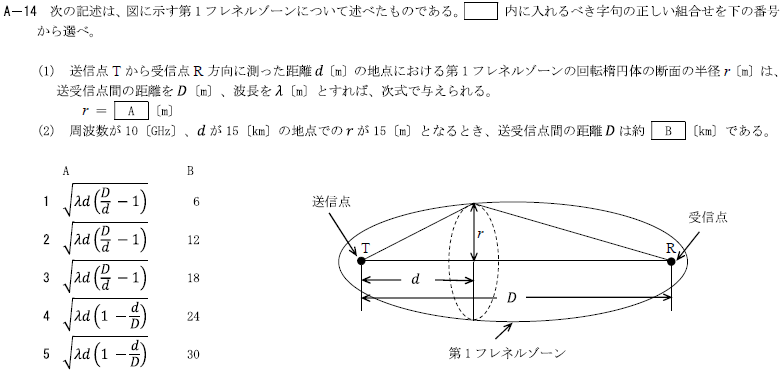
R4.07-1A14
5 \(\sqrt{λd(1-\frac{d}{D})} 30\)

第1フレネルゾーンの半径\(r\)は、\(r=5\sqrt{\frac{3D}{f}}\)[m]
\(r^2=5^2×\frac{3D}{f}\)
\(D=\frac{r^2f}{75}=\frac{15^2×10}{75}=30\)[km]
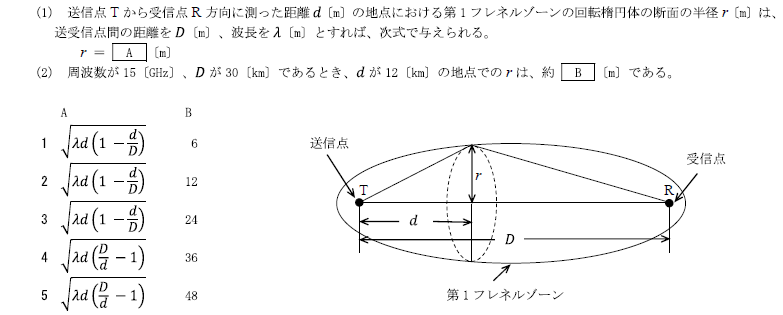
R3.01-1A17 穴埋め
2 \(\sqrt{λd(1-\frac{d}{D})} 12\)

第1フレネルゾーンの半径\(r\)は、\(r=5\sqrt{\frac{3D}{f}}\)[m]
\(r=5\sqrt{\frac{3×30}{15}}=5\sqrt{6}\) !?
上手くいかない時は、設問の式を使用します。
\(r=\sqrt{λd(1-\frac{d}{D})}\)
\(fλ=c\)より、\(λ=\frac{c}{f}=\frac{300M}{15G}=\frac{1}{50}\)[m]
\(D=30\)[km]、\(d=12\)[km]
\(\frac{d}{D}=\frac{12}{30}=\frac{2}{5}\)
\(r=\sqrt{λd(1-\frac{d}{D})}\)
\(=\sqrt{\frac{1}{50}×12k(1-\frac{2}{5})}=\sqrt{\frac{12k}{50}×\frac{3}{5}}=\sqrt{144}=12\)[m]
検索用キーワード(問題文の最初の一文)
図に示す第1フレネルゾーン


コメント