BR8.01出題予想
R5.07-2A7

R4.01-1A6
R2.11-1A6
解答
R5.07-2A7
3 0.29
ワンポイント解説
平行平板線路の\(\frac{d}{W}=0.37\log{\frac{b}{a}}\)
\(d\):誘電体厚さ[m]、\(W\):導体幅[m]、\(a\):内部導体外径[m]、\(b\):外部導体内径[m]

\(\log{\frac{b}{a}}=\log{6}=\log({2×3})=\log{2}+\log{3}=0.30+048=0.78\)
\(\frac{d}{W}=0.37\log{\frac{b}{a}}\)
\(=0.37×0.78=0.29\)
R4.01-1A6
1 0.22

\(\log{\frac{b}{a}}=\log{4}=\log({2^2})=2\log{2}=2×0.30=0.60\)
\(\frac{d}{W}=0.37\log{\frac{b}{a}}\)
\(=0.37×0.60=0.22\)
R2.11-1A6
2 0.26

\(\log{\frac{b}{a}}=\log{5}=\log({10÷2})=\log{10}-\log{2}=1-0.3=0.7\)
\(\frac{d}{W}=0.37\log{\frac{b}{a}}\)
\(=0.37×0.7=0.26\)
検索用キーワード(問題文の最初の一文)
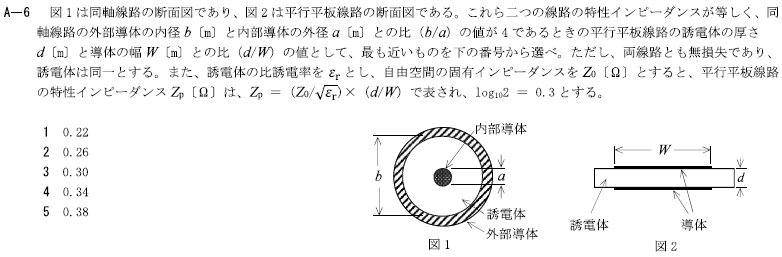
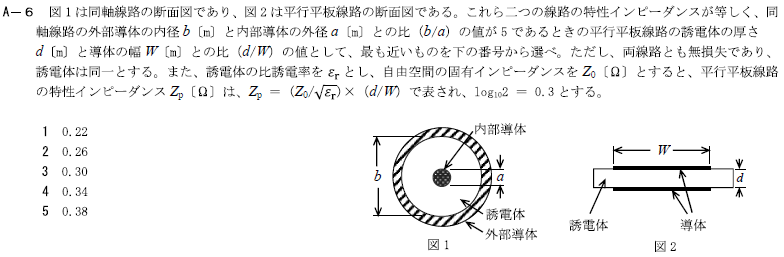
図1は同軸線路の断面図であり、図2は平行平板線路の断面図である。これら二つの線路の特性インピーダンスが等しく、同軸線路の外部導体の内径b[m]と内部導体の外形a[m]との比(b/a)の値が6であるときの平行平板線路の誘電体の厚さd[m]と導体の幅W[m]との比(d/W)の値


コメント