BR8.01出題予想
R5.01-2A6
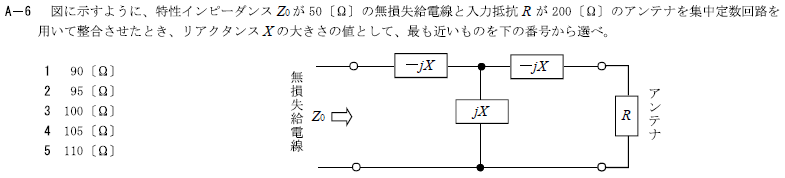
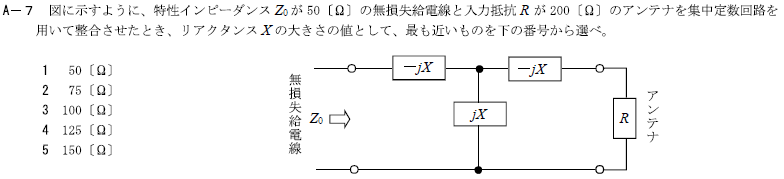
R5.01-1A7
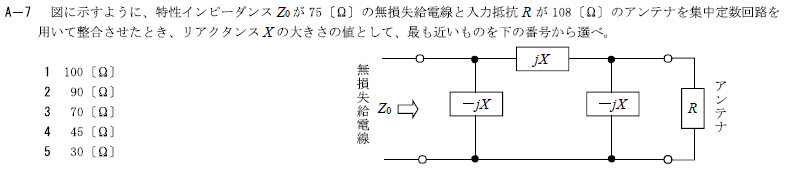
R4.01-2A6
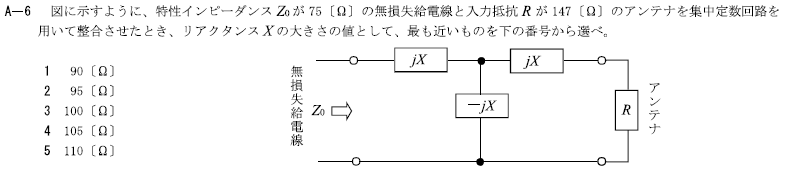
R3.07-2A7
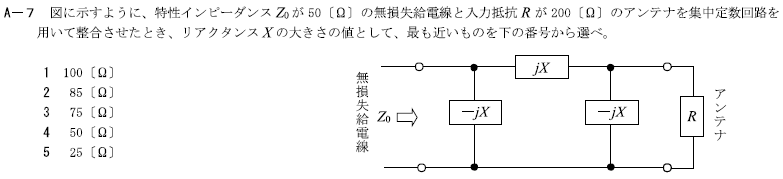
R2.11-1A7
解答
R5.01-2A6
3 100[Ω]
ワンポイント解説
集中定数回路リアクタンス\(X=\sqrt{R・Z_0}\) [Ω]

リアクタンス\(X=\sqrt{R・Z_0}\) [Ω]より
\(X=\sqrt{200×50}=\sqrt{10,000}=\sqrt{100^2}=100\)[Ω]
R5.01-1A7
2 90[Ω]

リアクタンス\(X=\sqrt{R・Z_0}\) [Ω]より
\(X=\sqrt{108×75}\)
素因数分解
\(108=2×2×3×3×3\)
\(75=3×5×5\)
\(X=\sqrt{108×75}\)
\(=\sqrt{2×2×3×3×3×3×5×5}\)
\(=\sqrt{2^2×3^2×3^2×5^2}\)
\(=90\)[Ω]
R4.01-2A6
4 105[Ω]

リアクタンス\(X=\sqrt{R・Z_0}\) [Ω]より
\(X=\sqrt{147×75}\)
素因数分解
\(147=3×7×7\)
\(75=3×5×5\)
\(X=\sqrt{147×75}\)
\(=\sqrt{3×7×7×3×5×5}\)
\(=\sqrt{3^2×7^2×5^2}\)
\(=105\)[Ω]
R3.07-2A7
1 100[Ω]

リアクタンス\(X=\sqrt{R・Z_0}\) [Ω]より
\(X=\sqrt{200×50}=\sqrt{10,000}=\sqrt{100^2}=100\)[Ω]
R2.11-1A7
3 100[Ω]

リアクタンス\(X=\sqrt{R・Z_0}\) [Ω]より
\(X=\sqrt{200×50}=\sqrt{10,000}=\sqrt{100^2}=100\)[Ω]
検索用キーワード(問題文の最初の一文)
図に示すように、特性インピーダンスZoが50[Ω]の無損失給電線と入力抵抗Rが200[Ω]のアンテナを集中定数回路を用いて整合させたとき、リアクタンスXの大きさの値
図に示すように、特性インピーダンスZoが75[Ω]の無損失給電線と入力抵抗Rが108[Ω]のアンテナを集中定数回路を用いて整合させたとき、リアクタンスXの大きさの値
図に示すように、特性インピーダンスZoが75[Ω]の無損失給電線と入力抵抗Rが147[Ω]のアンテナを集中定数回路を用いて整合させたとき、リアクタンスXの大きさの値
図に示すように、特性インピーダンスZoが50[Ω]の無損失給電線と入力抵抗Rが200[Ω]のアンテナを集中定数回路を用いて整合させたとき、リアクタンスXの大きさの値


コメント