AR8.01出題予想
R5.07-2A9
R4.07-1A6
R3.01-2A5

R7.01-1A7
R2.11-2A6
解答
R5.07-2A9
2 4 4 19.7
ワンポイント解説

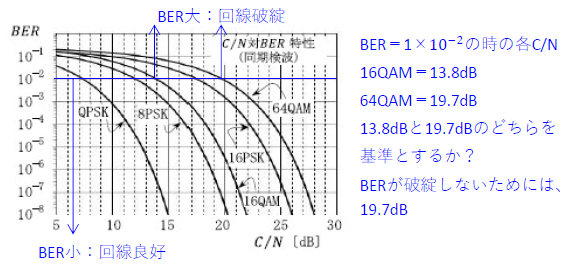
(1)\(BER=1×10^{-8}\)の時の各\(C/N\)は、グラフから
BPSK=?[dB]
QPSK=15[dB]
16QAM=22[dB]
また、
BPSKの誤差補関数=(1/2)erfc(\(\sqrt{C/N}\))
QPSKの誤差補関数=(1/2)erfc(\(\sqrt{(C/N)/2}\))が与えられており、
これは、同じBER(例えば\(BER=10^{-8}\))の場合、
QPSKのC/NはBPSKより2倍(+3[dB])高いと言うことです。
したがって、BPSKはQPSKより3[dB]低くなります。
BPSK=QPSK-3=15-3=12[dB]
QPSK=15[dB]
16QAM=22[dB]
そして、C/Nと\(E_b/N_0\)の関係は、
BPSK=C/N=\(E_b/N_0\)[dB]
QPSK=C/N=\(2E_b/N_0\)(真数)=3+\(E_b/N_0\)[dB]
16QAM=C/N=\(4E_b/N_0\)(真数)=6+\(E_b/N_0\)[dB]
となりますので、
BPSK=C/N=12[dB]=12\(E_b/N_0\)
QPSK=C/N=15[dB]=\(2E_b/N_0\)(真数)=3+\(E_b/N_0\)[dB]
16QAM=C/N=22[dB]=\(4E_b/N_0\)(真数)=6+\(E_b/N_0\)[dB]
したがって、
BPSK=12\(E_b/N_0\)
QPSK=12\(E_b/N_0\)[dB]
16QAM=16\(E_b/N_0\)[dB]
BPSKは、16QAMに比べて\(E_b/N_0\)は4[dB](=16-12[dB])低い。
(2)\(BER=1×10^{-8}\)の時の各\(C/N\)は、グラフから
64QAM=28[dB]
16QAM=22[dB]より、
64QAMは、16QAMに比べて\(C/N\)は6[dB](=28-22[dB])高い。
デシベル計算より、
6[dB]は4倍。
(3)
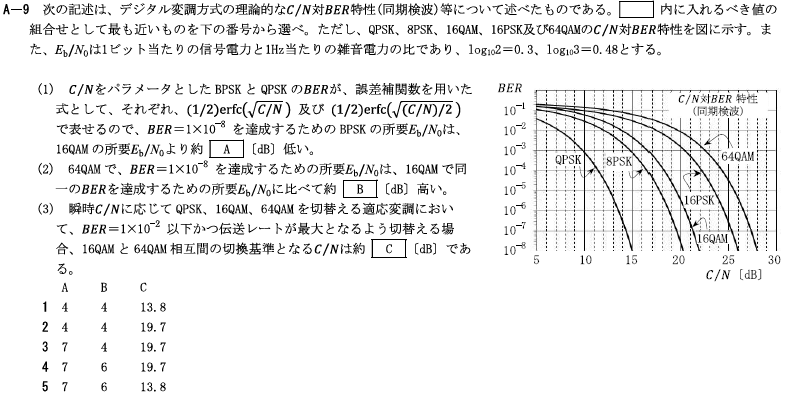
R4.07-1A6
3 4 25 15.5

(1)\(BER=1×10^{-8}\)の時の各\(C/N\)は、グラフから
64QAM=28[dB]
16QAM=22[dB]より、
64QAMは、16QAMに比べて\(C/N\)は6[dB](=28-22[dB])高い。
デシベル計算より、
6[dB]は4倍。
(2)\(BER=1×10^{-8}\)の時の各\(C/N\)は、グラフから
BPSK=?[dB]
QPSK=15[dB]
16PSK=26[dB]
また、
BPSKの誤差補関数=(1/2)erfc(\(\sqrt{C/N}\))
QPSKの誤差補関数=(1/2)erfc(\(\sqrt{(C/N)/2}\))が与えられており、
これは、同じBER(例えば\(BER=10^{-8}\))の場合、
QPSKのC/NはBPSKより2倍(+3[dB])高いと言うことです。
したがって、BPSKはQPSKより3[dB]低くなります。
BPSK=QPSK-3=15-3=12[dB]
QPSK=15[dB]
16PSK=26[dB]
したがって、
16PSKは、BPSKに比べて\(C/N\)は14[dB](=26-12[dB])高い。
デシベル計算より、
14[dB]は25倍。
(3)8PSKで、\(BER=1×10^{-8}\)を達成するための所要\(C/N=20.3\)[dB]
\(C/N=3E_b/N_0\)(真数の世界) \(\log_{10}3=0.48\)より、3倍は4.8[dB]なので
\(C/N=4.8+E_b/N_0\)(デシベルの世界)
\(E_b/N_0=C/N-4.8=20.3-4.8=15.5\)[dB]
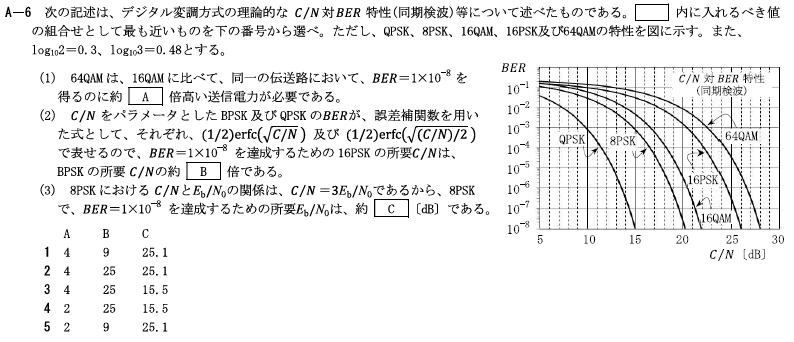
R3.01-2A5
3 8PSKにおける\(C/N\)と\(E_b/N_0\)(ビットエネルギー対雑音電力密度比)の関係は、\(C/N=3E_b/N_0\)であるから、8PSKで、\(BER=1×10^{-8}\)を達成するための所要\(E_b/N_0\)は、約25.1[dB] 約15.5[dB]である。
8PSKで、\(BER=1×10^{-8}\)を達成するための所要\(C/N=20.3\)[dB]
\(C/N=3E_b/N_0\)(真数の世界) \(\log_{10}3=0.48\)より、3倍は4.8[dB]なので
\(C/N=4.8+E_b/N_0\)(デシベルの世界)
\(E_b/N_0=C/N-4.8=20.3-4.8=15.5\)[dB]

1 \(BER=1×10^{-8}\)の時の各\(C/N\)は、グラフから
64QAM=28[dB]
16QAM=22[dB]より、
64QAMは、16QAMに比べて\(C/N\)は6[dB](=28-22[dB])高い。
デシベル計算より、
6[dB]は4倍。
2 グラフから読み取りそのまんまです。
4 \(BER=1×10^{-8}\)の時の各\(C/N\)は、グラフから
QPSK=15[dB]
16PSK=26[dB]より、
QPSKは、16PSKに比べて\(C/N\)は11[dB](=26-15[dB])低い。
5 \(BER=1×10^{-8}\)の時の各\(C/N\)は、グラフから
BPSK=?[dB]
QPSK=15[dB]
16PSK=26[dB]
また、
BPSKの誤差補関数=(1/2)erfc(\(\sqrt{C/N}\))
QPSKの誤差補関数=(1/2)erfc(\(\sqrt{(C/N)/2}\))が与えられており、
これは、同じBER(例えば\(BER=10^{-8}\))の場合、
QPSKのC/NはBPSKより2倍(+3[dB])高いと言うことです。
したがって、BPSKはQPSKより3[dB]低くなります。
BPSK=QPSK-3=15-3=12[dB]
QPSK=15[dB]
16PSK=26[dB]
したがって、
16PSKは、BPSKに比べて\(C/N\)は14[dB](=26-12[dB])の差がある。
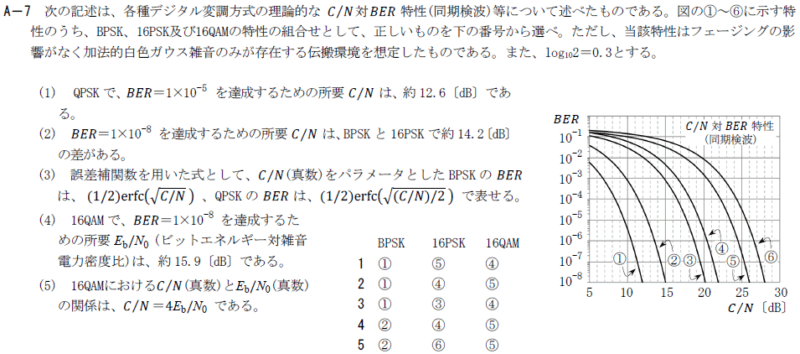
R7.01-1A7
1 ① ⑤ ④

■QPSKは、(1)より、②
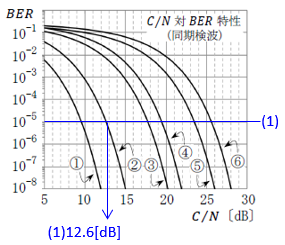
■BPSKは、(3)より、
BPSKの誤差補関数=(1/2)erfc(\(\sqrt{C/N}\))
QPSKの誤差補関数=(1/2)erfc(\(\sqrt{(C/N)/2}\))が与えられており、
これは、同じBER(例えば\(BER=10^{-8}\))の場合、
QPSKのC/NはBPSKより2倍(+3[dB])高いと言うことです。
したがって、BPSKはQPSKより3[dB]低い①になります。
■16PSKは、(2)より、
\(BER=1×10^{-8}\)の時の16PSKの\(C/N\)は、BPSKより14.2[dB]高いので
16PSK=BPSK+14.2[dB]
16PSK=12+14.2[dB]=26.2[dB]より、⑤
■(4)(5)より、16QAMで、\(BER=1×10^{-8}\)を達成するための所要\(E_b/N_0=\)15.9[dB]
\(C/N=4E_b/N_0\)(真数の世界) より、4倍は6[dB]なので
\(C/N=6+E_b/N_0[dB]=6+15.9=21.9\)[dB]より、④
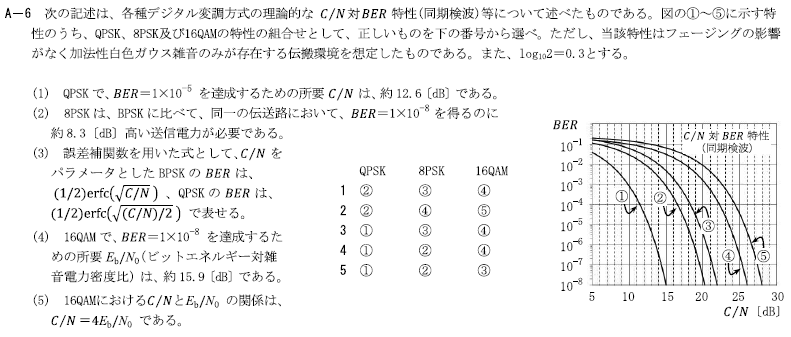
R2.11-2A6
5 ① ② ③

■QPSKは、(1)より、①
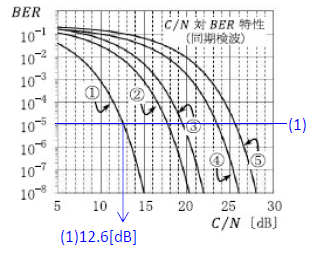
■BPSKは、(3)より、
BPSKの誤差補関数=(1/2)erfc(\(\sqrt{C/N}\))
QPSKの誤差補関数=(1/2)erfc(\(\sqrt{(C/N)/2}\))が与えられており、
これは、同じBER(例えば\(BER=10^{-8}\))の場合、
QPSKのC/NはBPSKより2倍(+3[dB])高いと言うことです。
したがって、BPSKはQPSKより3[dB]低いので、
BPSK=15(QPSK)-3=12[dB]になります。 ※グラフには無いです。
■8PSKは、(2)より、
\(BER=1×10^{-8}\)の時の8PSKの\(C/N\)は、BPSKより8.3[dB]高いので
8PSK=BPSK+8.3[dB]
8PSK=12+8.3[dB]=20.3[dB]より、②
■(4)(5)より、16QAMで、\(BER=1×10^{-8}\)を達成するための所要\(E_b/N_0=\)15.9[dB]
\(C/N=4E_b/N_0\)(真数の世界) より、4倍は6[dB]なので
\(C/N=6+E_b/N_0[dB]=6+15.9=21.9\)[dB]より、③
検索用キーワード(問題文の最初の一文)
・デジタル変調方式の理論的なC/N対BER特性(同期検波)等
・各種デジタル変調方式の理論的なC/N対BER特性(同期検波)等


コメント