AR8.01出題予想
R6.07-1B4

R4.07-1B4

R2.01-1B4
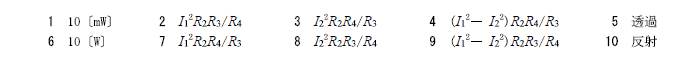
R3.01-1A20

解答
R6.07-1B4
1 10[mW]
2 \(I_1^2R_2R_3/R_4\)
8 \(I_2^2R_2R_3/R_4\)
9 \((I_1^2-I_2^2)R_2R_3/R_4\)
10 反射
ワンポイント解説
(1)サーミスタ電力計って10[mW]程度しか使用出来ません。
テレビのミニサテでも使用不可ですね。
(2)求める電力\(P_1\)は、
\(P_1=R_1×I_1^2\) ← \(電力P=電圧V×電流I=抵抗R×電流I^2\)
ブリッジが平衡状態(G=0)ならば、
対角線の抵抗の積 \(R_1×R_4=R_2×R_3\) となるので、
\(P_1=R_1×I_1^2=I_1^2×\frac{R_2R_3}{R_4}\)
(3)求める電力\(P_2\)は、電流が\(I_1\)から\(I_2\)に変わっただけですので、(2)と同様に
\(P_2=R_1×I_2^2=I_2^2×\frac{R_2R_3}{R_4}\)
(4)求める電力\(P_m\)は、(2)と(3)より
\(P_m=P_1-P_2=I_1^2×\frac{R_2R_3}{R_4}-I_2^2×\frac{R_2R_3}{R_4}\)
\(=(I_1^2-I_2^2)\frac{R_2R_3}{R_4}\)
(5)導波管(ケーブル類)と負荷設備(電力計含む)などの不整合ときたら、反射が生じます。

R4.07-1B4
6 10[mW]
7 \(I_1^2R_2R_3/R_4\)
3 \(I_2^2R_2R_3/R_4\)
4 \((I_1^2-I_2^2)R_2R_3/R_4\)
5 反射

R2.01-1B4
1 10[mW]
2 \(I_1^2R_2R_3/R_4\)
8 \(I_2^2R_2R_3/R_4\)
9 \((I_1^2-I_2^2)R_2R_3/R_4\)
10 反射
R3.01-1A20
1 10[mW] \(I_1^2R_2R_4/R_3\) \((I_1^2-I_2^2)R_2R_4/R_3\)

ワンポイント解説
解き方は同上ですが、同上と比べると、ブリッジ回路の抵抗番号が変更されています。
ブリッジが平衡状態(G=0)ならば、
対角線の抵抗の積 \(R_1×R_3=R_2×R_4\) となる事を押さえておきましょう。
検索用キーワード(問題文の最初の一文)
・図に示すマイクロ波用サーミスタ電力計の動作原理



コメント