AR8.01出題予想
R4.07-2A15
R3.01-1A13
H31.01-1A16
解答
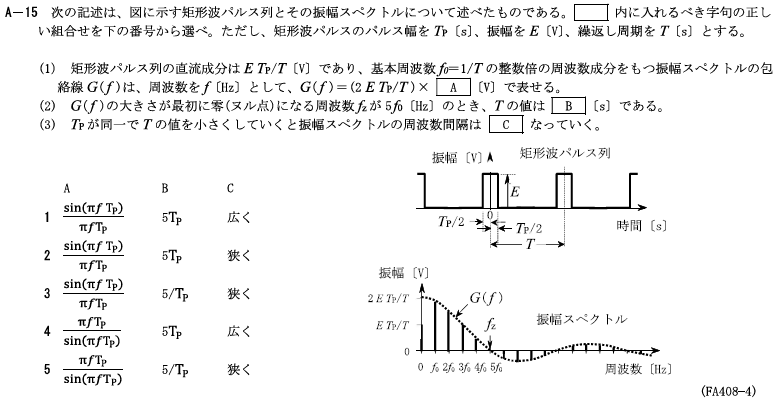
R4.07-2A15
1 \(\frac{\sin{(πfT_P)}}{πfT_P} 5T_P\) 広く
ワンポイント解説
図で覚えちゃいましょう。

↑ハープに見えません?

\(f_Z=nf_0=n×\frac{1}{T}=\frac{1}{T_P}\)より、
\(f_Z=5f_0=5×\frac{1}{T}=\frac{1}{T_P}\)
\(T=5T_P\)
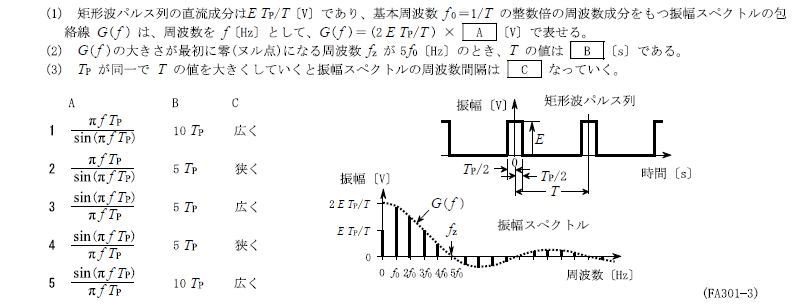
R3.01-1A13
4 \(\frac{\sin{(πfT_P)}}{πfT_P} 5T_P\) 狭く

\(f_Z=nf_0=n×\frac{1}{T}=\frac{1}{T_P}\)より、
\(f_Z=5f_0=5×\frac{1}{T}=\frac{1}{T_P}\)
\(T=5T_P\)
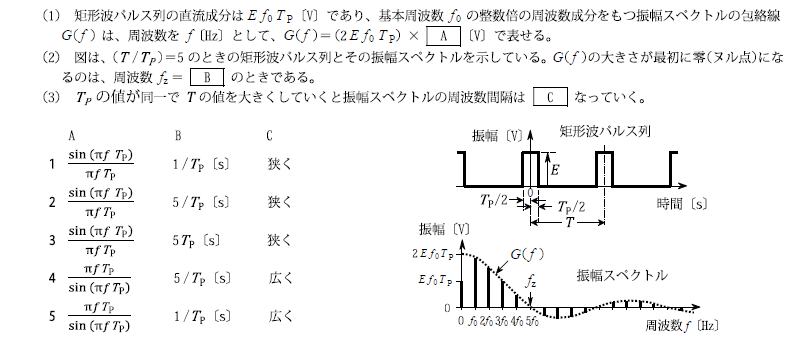
H31.01-1A16
1 \(\frac{\sin{(πfT_P)}}{πfT_P} 1/T_P\)[s] 狭く

\(f_Z=nf_0=n×\frac{1}{T}=\frac{1}{T_P}\)より、
\(\frac{T}{T_P}=5=n\)なので、\(n=5\)を代入すると、
\(f_Z=5f_0=5×\frac{1}{T}=\frac{1}{T_P}\)
結局、\(f_Z=\frac{1}{T_P}\)[s]なんですね。。。
検索用キーワード(問題文の最初の一文)
・図に示す矩形波パルス列とその振幅スペクトル


コメント