AR8.01出題予想
R5.07-2A12

R4.07-2A12

R3.07-1A12

H31.01-1A13

R4.01-1A12

R2.11-2A10

R1.07-1A13

解答
R5.07-2A12
3 20[km]
ワンポイント解説
最大探知距離\(R=(\frac{P_TGρA_e}{4^2π^2P_R})^{\frac{1}{4}}\)[m]
\(P_T\):送信尖頭出力[W]
\(G\):アンテナ利得[真数]
\(ρ\)(ロー):有効反射断面積[㎡]
\(A_e\):アンテナの実効面積[㎡]
\(P_R\):受信電力[W]
※[dB]は真数に変換して代入します。

先ずは、デシベル計算
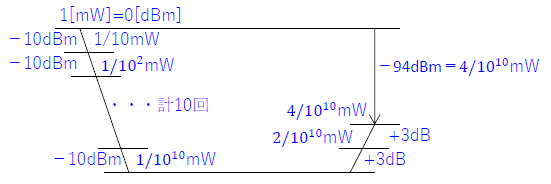
最大探知距離\(R=(\frac{P_TGρA_e}{4^2π^2P_R})^{\frac{1}{4}}\)[m]
Gは\(A=Gλ^2/(4π)\)より、\(G=4πA/λ^2\)
λは\(fλ=c\)より、\(λ=\frac{c}{f}\)
改めてGは、\(G=4πA(\frac{f}{c})^2\)
\(R=(\frac{P_T×4πA(\frac{f}{c})^2×ρA_e}{4^2π^2P_R})^{\frac{1}{4}}\)
\(=(\frac{P_T×A×(\frac{f}{c})^2×ρA_e}{4πP_R})^{\frac{1}{4}}\)
\(=(\frac{1k×1.6×(\frac{3G}{300M})^2×π×1.6}{4π×\frac{4}{10^{10}}m})^{\frac{1}{4}}\)
\(=(\frac{1k×16×16}{4×\frac{4}{10^{13}}})^{\frac{1}{4}}\)
\(=(2^4×10^{16})^{\frac{1}{4}}\)
\(=2×10^4=20\)[km]
R4.07-2A12
1 10[km]

先ずは、デシベル計算
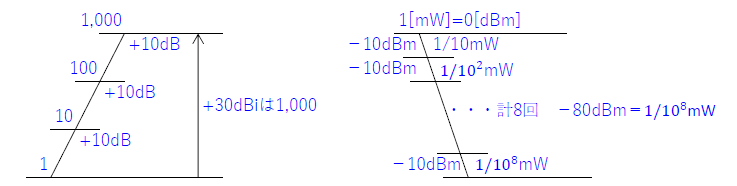
最大探知距離\(R=(\frac{P_TGρA_e}{4^2π^2P_R})^{\frac{1}{4}}\)[m]
\(=(\frac{1,000×1,000×π^2×1.6}{4^2π^2×\frac{1}{10^8}m})^{\frac{1}{4}}\)
\(=(\frac{10^6×1.6}{4^2×\frac{1}{10^{11}}})^{\frac{1}{4}}\)
\(=(\frac{16×10^{16}}{16})^{\frac{1}{4}}\)
\(=10^4[m]=10[km]\)
R3.07-1A12
2 50[km]

先ずは、デシベル計算

最大探知距離\(R=(\frac{P_TGρA_e}{4^2π^2P_R})^{\frac{1}{4}}\)[m]
Gは\(A=Gλ^2/(4π)\)より、\(G=4πA/λ^2\)
λは\(fλ=c\)より、\(λ=\frac{c}{f}\)
改めてGは、\(G=4πA(\frac{f}{c})^2\)
\(R=(\frac{P_T×4πA(\frac{f}{c})^2×ρA_e}{4^2π^2P_R})^{\frac{1}{4}}\)
\(=(\frac{P_T×A×(\frac{f}{c})^2×ρA_e}{4πP_R})^{\frac{1}{4}}\)
\(=(\frac{100k×1×(\frac{3G}{300M})^2×π×1}{4π×\frac{4}{10^{10}}m})^{\frac{1}{4}}\)
\(=(\frac{100k×10^2}{4×\frac{4}{10^{13}}})^{\frac{1}{4}}\)
\(=(\frac{10^{20}}{2^4})^{\frac{1}{4}}\)
\(=\frac{10^5}{2}\)
\(=\frac{100k}{2}=50\)[km]
H31.01-1A13
1 100[km]

先ずは、デシベル計算

最大探知距離\(R=(\frac{P_TGρA_e}{4^2π^2P_R})^{\frac{1}{4}}\)[m]
\(=(\frac{10k×10,000×π^2×1.6}{4^2π^2×\frac{1}{10^{10}}m})^{\frac{1}{4}}\)
\(=(\frac{16×10^7}{16×\frac{1}{10^{13}}})^{\frac{1}{4}}\)
\(=(10^{20})^{\frac{1}{4}}\)
\(=10^5[m]=100[km]\)
R4.01-1A12
4 1.4 1.4 1.7
ワンポイント解説
最大探知距離\(R=(\frac{P_TGρA_e}{4^2π^2P_R})^{\frac{1}{4}}\)[m]
\(P_T\):送信尖頭出力[W]
\(G\):アンテナ利得[真数]
\(ρ\)(ロー):有効反射断面積[㎡]
\(A_e\):アンテナの実効面積[㎡]
\(P_R\):受信電力[W]
※[dB]は真数に変換して代入します。

\(R=(\frac{P_TGρA_e}{4^2π^2P_R})^{\frac{1}{4}}\)[m]
(1)\(P_R=0.25\)倍の時、
\(R=(\frac{P_TGρA_e}{4^2π^2×0.25P_R})^{\frac{1}{4}}\)[m]
0.25倍だけ着目すると、
\(R=(\frac{1}{0.25})^{\frac{1}{4}}\)
\(=(\frac{1}{\frac{1}{4}})^{\frac{1}{4}}\)
\(=(2^2)^{\frac{1}{4}}\)
\(=2^{\frac{1}{2}}=\sqrt{2}=1.4\)
(2)\(P_T=8\)倍、\(P_R=2\)倍の時、
\(R=(\frac{8P_TGρA_e}{4^2π^2×2P_R})^{\frac{1}{4}}\)[m]
8倍と2倍だけ着目すると、
\(R=(\frac{8}{2})^{\frac{1}{4}}\)
\(=(2^2)^{\frac{1}{4}}\)
\(=2^{\frac{1}{2}}=\sqrt{2}=1.4\)
(3)\(ρ=9\)倍の時、
\(R=(\frac{P_TG9ρA_e}{4^2π^2P_R})^{\frac{1}{4}}\)[m]
9倍だけ着目すると、
\(R=(9)^{\frac{1}{4}}\)
\(=(3^2)^{\frac{1}{4}}\)
\(=3^{\frac{1}{2}}=\sqrt{3}=1.7\)
R2.11-2A10
1 1.4 2.0 1.4

\(R=(\frac{P_TGρA_e}{4^2π^2P_R})^{\frac{1}{4}}\)[m]
(1)\(P_R=0.25\)倍の時、
\(R=(\frac{P_TGρA_e}{4^2π^2×0.25P_R})^{\frac{1}{4}}\)[m]
0.25倍だけ着目すると、
\(R=(\frac{1}{0.25})^{\frac{1}{4}}\)
\(=(\frac{1}{\frac{1}{4}})^{\frac{1}{4}}\)
\(=(2^2)^{\frac{1}{4}}\)
\(=2^{\frac{1}{2}}=\sqrt{2}=1.4\)
(2)\(P_T=16\)倍の時、
\(R=(\frac{16P_TGρA_e}{4^2π^2P_R})^{\frac{1}{4}}\)[m]
16倍だけ着目すると、
\(R=(16)^{\frac{1}{4}}\)
\(=(2^4)^{\frac{1}{4}}\)
\(=2^1=2.0\)
(3)\(ρ=4\)倍の時、
\(R=(\frac{P_TG4ρA_e}{4^2π^2P_R})^{\frac{1}{4}}\)[m]
4倍だけ着目すると、
\(R=(4)^{\frac{1}{4}}\)
\(=(2^2)^{\frac{1}{4}}\)
\(=2^{\frac{1}{2}}=\sqrt{2}=1.4\)
R1.07-1A13
3 0.7 2.0 1.4

\(R=(\frac{P_TGρA_e}{4^2π^2P_R})^{\frac{1}{4}}\)[m]
(1)\(P_R=4\)倍の時、
\(R=(\frac{P_TGρA_e}{4^2π^2×4P_R})^{\frac{1}{4}}\)[m]
4倍だけ着目すると、
\(R=(\frac{1}{4})^{\frac{1}{4}}\)
\(=(\frac{1}{2^2})^{\frac{1}{4}}\)
\(=(2^{-2})^{\frac{1}{4}}\)
\(=2^{-\frac{1}{2}}=\frac{1}{\sqrt{2}}=0.7\)
(2)\(P_T=16\)倍の時、
\(R=(\frac{16P_TGρA_e}{4^2π^2P_R})^{\frac{1}{4}}\)[m]
16倍だけ着目すると、
\(R=(16)^{\frac{1}{4}}\)
\(=(2^4)^{\frac{1}{4}}\)
\(=2^1=2.0\)
(3)\(ρ=4\)倍の時、
\(R=(\frac{P_TG4ρA_e}{4^2π^2P_R})^{\frac{1}{4}}\)[m]
4倍だけ着目すると、
\(R=(4)^{\frac{1}{4}}\)
\(=(2^2)^{\frac{1}{4}}\)
\(=2^{\frac{1}{2}}=\sqrt{2}=1.4\)
検索用キーワード(問題文の最初の一文)
・レーダー方程式を用いて求めたパルスレーダーの最大探知距離の値
・レーダー方程式において、送信電力等のパラメータを変えた時の最大探知距離(\(R_{max}\))の変化


コメント