R4.10b-20
次の記述は、自由空間における電波伝搬について述べたものである。( )内に入れるべき字句の正しい組合せを下の番号から選べ。
(1) 等方性アンテナから、距離\(d〔m〕\)のところにおける自由空間電界強度\(E〔V/m〕\)は、放射電力を\(P〔W〕\)とすると、次式で表される。
\(E=\frac{\sqrt{30P}}{d} [V/m]\)
また、半波長ダイポールアンテナに対する相対利得\(G\)(真数)のアンテナの場合、最大放射方向における自由空間電界強度\(E_r〔V/m〕\)は、次式で表される。
\(E_r≒( A ) [V/m]\)
(2) 半波長ダイポールアンテナに対する相対利得が14〔dB〕の指向性アンテナに、4〔W〕の電力を供給した場合、最大放射方向で送信点からの距離が12.5〔km〕の受信点における電界強度の値は、約( B )〔V/m〕である。ただし、アンテナ及び給電系の損失はないものとし、\(\log_{10}{2}\)の値は0.3とする。
A B
1 \(\frac{7\sqrt{GP}}{d}\) \(4.0×10^{-3}\)
2 \(\frac{7\sqrt{GP}}{d}\) \(5.6×10^{-3}\)
3 \(\frac{G\sqrt{30P}}{d}\) \(17.5×10^{-3}\)
4 \(\frac{G\sqrt{30P}}{d}\) \(21.9×10^{-3}\)
解答
2 \(\frac{7\sqrt{GP}}{d}\) \(5.6×10^{-3}\)
(1) 等方性アンテナから、距離\(d〔m〕\)のところにおける自由空間電界強度\(E〔V/m〕\)は、放射電力を\(P〔W〕\)とすると、次式で表される。
\(E=\frac{\sqrt{30P}}{d} [V/m]\)
また、半波長ダイポールアンテナに対する相対利得\(G\)(真数)のアンテナの場合、最大放射方向における自由空間電界強度\(E_r〔V/m〕\)は、次式で表される。
\(E_r≒\)( \(\frac{7\sqrt{GP}}{d}\) ) \([V/m]\)
(2) 半波長ダイポールアンテナに対する相対利得が14〔dB〕の指向性アンテナに、4〔W〕の電力を供給した場合、最大放射方向で送信点からの距離が12.5〔km〕の受信点における電界強度の値は、約( \(5.6×10^{-3}\) )〔V/m〕である。ただし、アンテナ及び給電系の損失はないものとし、\(\log_{10}{2}\)の値は0.3とする。
解き方
\(E_r≒\frac{7\sqrt{GP}}{d} [V/m]\) は真数の式なので
①半波長ダイポールアンテナに対する相対利得の14〔dB〕をデシベル計算で真数にする。
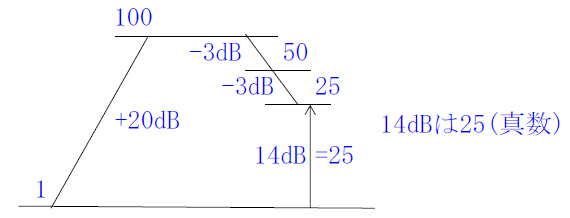
②\(E_r\)の式を使用する
\(E_r≒\frac{7\sqrt{GP}}{d}\)
\(E_r≒\frac{7\sqrt{25×4}}{12.5k}=\frac{7\sqrt{10^2}}{12.5k}=\frac{70}{12.5k}=5.6×10^{-3} [V/m]\)


コメント