R5.01-1B5 B穴埋め

R2.11-2B5 B穴埋め

R3.07-1A17

解答
R5.01-1B5
ア 1:3
イ 7:\(\frac{1}{3\sqrt{2}}I_m\)
ウ 3:実効値
エ 4:\(\frac{\sqrt{5}}{3}I_m\)
オ 5:\(\frac{π}{2\sqrt{2}}\)

(1) \(i\)は、基本波に、最大値が基本波の\(\frac{1}{3}\)で周波数が基本波の( 3 )倍の高調波が加わった電流である。
\(i=I_m\sin{ωt}(←基本波)+\frac{1}{3}I_m\sin{3ωt}(←高調波) [A]\)
\(ω=2πfより、f=\frac{ω}{2π}\)
基本波の周波数:\(f=\frac{ω}{2π}\)
高調波の周波数:\(f=\frac{3ω}{2π}\)より、
高調波の周波数は基本波の3倍です。
(2) 周波数が基本波の( 3 )倍の高調波の電流の実効値は、( \(\frac{1}{3\sqrt{2}}I_m\) )[A]である。
ワンポイント解説
最大値を\(I_m\)、平均値を\(I_a\)、実効値を\(I_e\)とすると、
(m=Max、a=Average、e=Effective)
・平均値\(I_a=\frac{2}{π}I_m\)
・実効値\(I_e=\frac{1}{\sqrt{2}}I_m\)
周波数が基本波の( 3 )倍の高調波の電流の実効値は、
振幅が\(\frac{1}{3}I_m\)なので、
実効値\(I_e=\frac{1}{\sqrt{2}}×\frac{1}{3}I_m=\frac{1}{3\sqrt{2}}I_m\)
(3) 熱電対形電流計\(A_1\)は、\(i\)の( 実効値 )を指示し、その値は( \(\frac{\sqrt{5}}{3}I_m\) )[A]である。
ワンポイント解説
基本波と高調波の実効値を求めるときは、
基本波と高調波の実効値を求めて、
\(実効値=\sqrt{(基本波の実効値)^2+(高調波の実効値)^2}\)
基本波の実効値\(I_e=\frac{1}{\sqrt{2}}I_m\)
高調波の実効値は、(2)より、\(\frac{1}{3\sqrt{2}}I_m\)
求める基本波と高調波の実効値は、
\(実効値=\sqrt{(基本波の実効値)^2+(高調波の実効値)^2}\)
\(=\sqrt{(\frac{1}{\sqrt{2}}I_m)^2+(\frac{1}{3\sqrt{2}}I_m)^2}=\sqrt{\frac{1}{2}I_m^2+\frac{1}{18}I_m^2}\)
\(=\sqrt{\frac{10}{18}I_m^2}=\sqrt{\frac{5}{9}I_m^2}=\frac{\sqrt{5}}{3}I_m\)
(4) 整流形電流計\(A_2\)は、\(i\)の平均値の( \(\frac{π}{2\sqrt{2}}\) )倍の値を指示する。
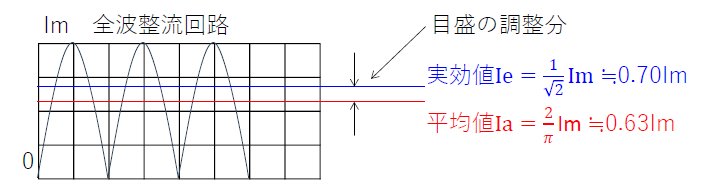
整流形電流計\(A_2\)は、平均値を測定します。
問題文では、目盛は実効値を示すように調整しました。
よって、指示値(実効値)は平均値の何倍かを求めます。
ワンポイント解説
最大値を\(I_m\)、平均値を\(I_a\)、実効値を\(I_e\)とすると、
(m=Max、a=Average、e=Effective)
・平均値\(I_a=\frac{2}{π}I_m\)
・実効値\(I_e=\frac{1}{\sqrt{2}}I_m\)
平均値\(I_a=\frac{2}{π}I_m\)より、\(I_m=\frac{平均値}{\frac{2}{π}}\)
実効値\(I_e=\frac{1}{\sqrt{2}}I_m\)より、
\(=\frac{1}{\sqrt{2}}×\frac{平均値}{\frac{2}{π}}=\frac{π}{2\sqrt{2}}×平均値\)
R2.11-2B5 B穴埋め
ア 1:3
イ 7:\(\frac{1}{3\sqrt{2}}I_m\)
ウ 3:実効値
エ 4:\(\frac{\sqrt{5}}{3}I_m\)
オ 10:\(\frac{π}{2\sqrt{2}}\)
R3.07-1A17
\(5 \frac{4\sqrt{2}V_m}{9R}\)

整流形電流計は、平均値を測定します。
問題文では、目盛は実効値を示すように調整しました。
ワンポイント解説
最大値を\(I_m\)、平均値を\(I_a\)、実効値を\(I_e\)とすると、
(m=Max、a=Average、e=Effective)
・平均値\(I_a=\frac{2}{π}I_m\)
・実効値\(I_e=\frac{1}{\sqrt{2}}I_m\)
①基本波の平均値\(I_a=\frac{2}{π}I_m\)より、\(I_m=\frac{平均値}{\frac{2}{π}}\)
実効値\(I_e=\frac{1}{\sqrt{2}}I_m\)より、
\(=\frac{1}{\sqrt{2}}×\frac{平均値}{\frac{2}{π}}=\frac{π}{2\sqrt{2}}×平均値I_a\)
②平均値\(I_a\)を求める。
手順:\(V_{ab}\)の平均値を求め、オームの法則で\(I_a\)を求める。
2-1 \(V_{ab}\)の平均値を求める。
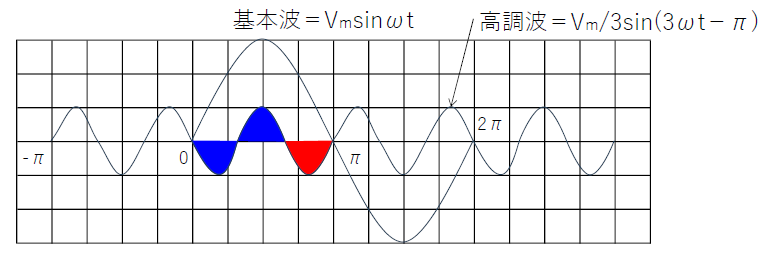
・基本波の平均値\(V_基=\frac{2}{π}V_m\)
・高調波の平均値は青色部分は打ち消すので0、赤色を求める。
高調波の平均値\(V_高=\frac{2}{π}×\frac{1}{3}V_m×\frac{1}{3}=\frac{2}{9π}V_m\)
(↑一番右の\(\frac{1}{3}\)は高調波の3つの山(青×2、赤×1)の内、赤色のみの事です。)
\(V_{ab}\)の平均値を求める。
\(V_{ab}=基本波平均値V_基+高調波平均値V_高=\frac{2}{π}V_m+(-\frac{2}{9π}V_m)\)
高調波分が\(-\)となるのは、高調波(赤色)は基本波に対して、
打ち消し合う向きとなっているからです。
\(V_{ab}=\frac{18-2}{9π}V_m=\frac{16}{9π}V_m\)
2-2 オームの法則で\(I_a\)を求める。
\(I_a=\frac{V_{ab}}{R}=\frac{16}{9π}V_m×\frac{1}{R}=\frac{16}{9πR}V_m\)
③求める実効値\(I_e=\frac{π}{2\sqrt{2}}×平均値=\frac{π}{2\sqrt{2}}×\frac{16}{9πR}V_m=\frac{8}{9\sqrt{2}R}V_m=\frac{4\sqrt{2}}{9R}V_m\)
検索用キーワード(問題文の最初の一文)
ひずみ波交流電流\(i=I_m\sin{ωt}+\frac{1}{3}I_m\sin{3ωt}\)[A]を熱電対形電流計\(A_1\)と整流形電流計\(A_2\)を用いて測定したときの指示値
図に示す回路の端子\(ab\)間に次式に示すひずみ波交流電圧\(v_{ab}\)を加えたとき、整流形電流計\(A\)の指示値


コメント