R5.07-1A14
R3.01-1A15
R4.01-2A14
R1.07-1A14
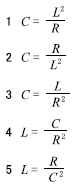
解答
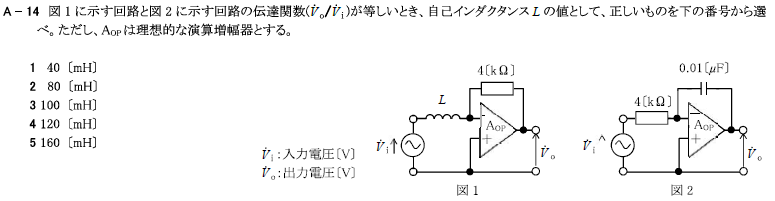
R5.07-1A14
５ 160［mH］
ワンポイント解説
伝達関数 \(L=CR^2\) \(L:\)自己インダクタンス \(C:\)コンデンサ \(R:\)抵抗
伝達（関数）で得るのは（L=）、ＣＲの事情（二乗）
伝達関数 \(L=CR^2=0.01×10^{-6}×(4×10^3)^2=16×10^{-8}×10^{6}=16×10^{-2}=160mH\)
R3.01-1A15
１ 160［mH］
R4.01-2A14
\(２ C=\frac{L}{R^2}\)
伝達関数 \(L=CR^2\)より、\(C=\frac{L}{R^2}\)
R1.07-1A14
\(３ C=\frac{L}{R^2}\)
検索用キーワード（問題文の最初の一文）
図１に示す回路と図２に示す回路の伝達関数（\(\dot{V}_o / \dot{V}_i\)）が等しいとき、自己インダクタンスLの値
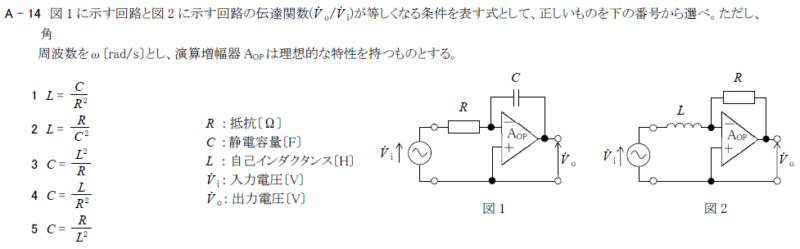
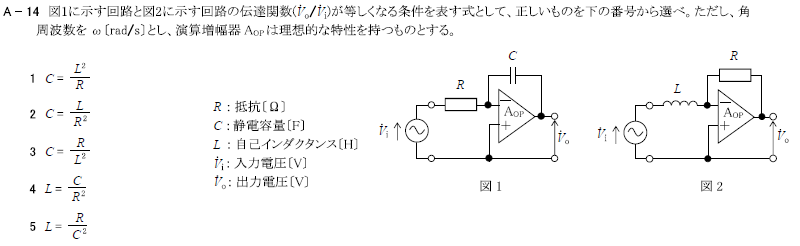
図１に示す回路と図２に示す回路の伝達関数（\(\dot{V}_o / \dot{V}_i\)）が等しくなる条件を表す式
コメント