R7.07-1A7
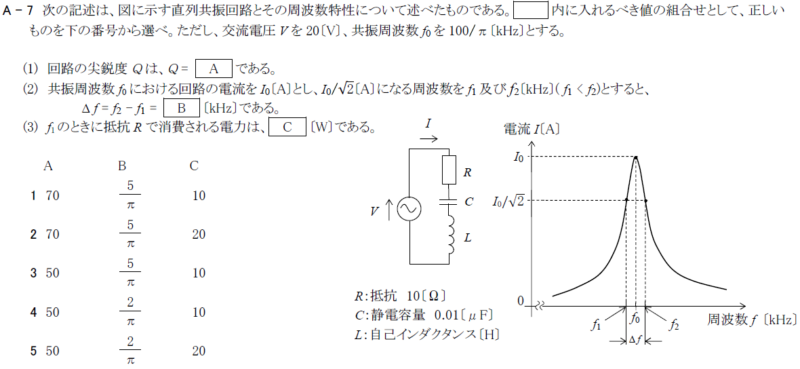
R3.01-2A7
解答
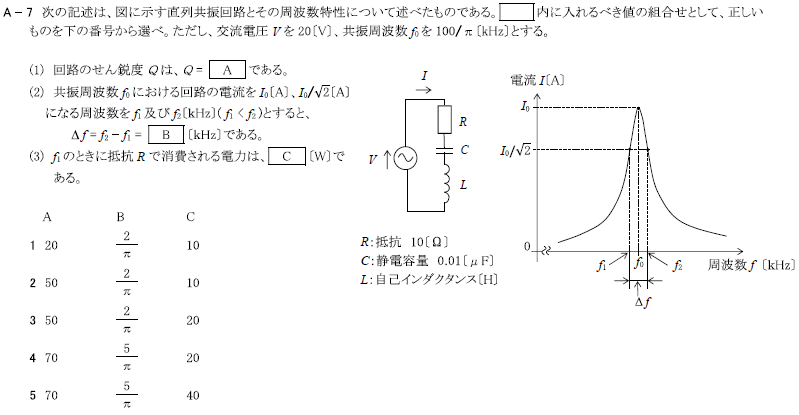
R7.07-1A7
\(5 50 \frac{2}{π} 20\)
ワンポイント解説
共振周波数\(f_0=\frac{1}{2π\sqrt{LC}}\)
尖鋭度\(Q=\frac{ω_OL}{R}=\frac{1}{ω_OCR}=\frac{f_0}{B}\)
帯域幅\(B=f2−f1=\frac{f_0}{Q}\)
\(f_0\)の消費電力\(P_0=I_0^2R\)
\(f_1\)の消費電力\(P_{f1}=\frac{I_0^2R}{2}\)

共振周波数\(f_0=\frac{100}{π}k[Hz]\)
尖鋭度\(Q=\frac{ω_OL}{R}=\frac{1}{ω_OCR}=\frac{1}{2πf_0CR}=\frac{1}{2π×\frac{100}{π}k×0.01μ×10}=\frac{1}{2×10^{-2}}=50\)
帯域幅\(B=f2−f1=\frac{f_0}{Q}=\frac{\frac{100}{π}k}{50}=\frac{2}{π}[kHz]\)
\(f_0\)の消費電力\(P_0=I_0^2R=(\frac{V}{R})^2R=\frac{V^2}{R}=\frac{20^2}{10}=40[W]\)
\(f_1\)の消費電力\(P_{f1}=\frac{I_0^2R}{2}=\frac{P_0}{2}=\frac{40}{2}=20[W]\)
R3.01-2A7
\(3 50 \frac{2}{π} 20\)

問題と解は同上
検索用キーワード(問題文の最初の一文)
図に示す直列共振回路とその周波数特性


コメント