R7.01-1A5

R5.01-2A5
R4.01-2A5

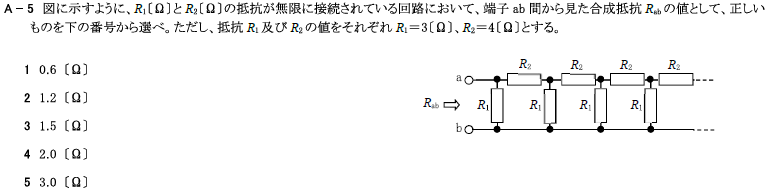
R2.11-1A5
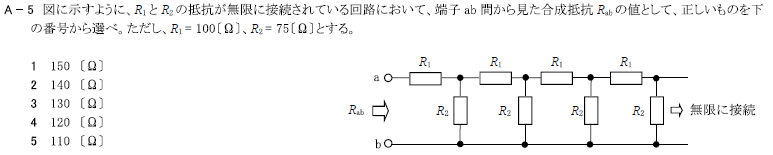
H31.01-1A5

解答
R7.01-1A5
5 120[Ω]
ワンポイント解説
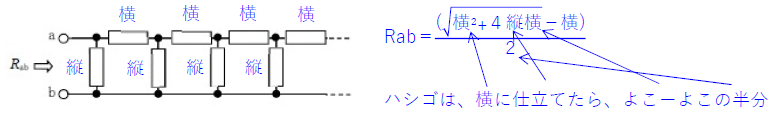

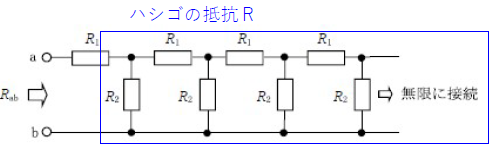
\(R=\frac{\sqrt{横^2+4縦横} -横}{2}=\frac{\sqrt{R_1^2+4R_2R_1}-R_1}{2}\)
\(=\frac{\sqrt{100^2+4×24×100}-100}{2}=\frac{\sqrt{19600}-100}{2}=\frac{140-100}{2}=20\)[Ω]
\(R_{ab}=R_1+R=100+20=120\)[Ω]
R5.01-2A5
4 2.0[Ω]


\(R_{ab}=\frac{\sqrt{横^2+4縦横} -横}{2}=\frac{\sqrt{R_2^2+4R_1R_2}-R_2}{2}\)
\(=\frac{\sqrt{4^2+4×3×4}-4}{2}=\frac{\sqrt{64}-4}{2}=2\)[Ω]
R4.01-2A5
5 300[Ω]


\(R=\frac{\sqrt{横^2+4縦横} -横}{2}=\frac{\sqrt{R_1^2+4R_2R_1}-R_1}{2}\)
\(=\frac{\sqrt{200^2+4×150×200}-200}{2}=\frac{\sqrt{160000}-200}{2}=\frac{400-200}{2}=100\)[Ω]
\(R_{ab}=R_1+R=200+100=300\)[Ω]
R2.11-1A5
1 150[Ω]


\(R=\frac{\sqrt{横^2+4縦横} -横}{2}=\frac{\sqrt{R_1^2+4R_2R_1}-R_1}{2}\)
\(=\frac{\sqrt{100^2+4×75×100}-100}{2}=\frac{\sqrt{40000}-100}{2}=\frac{200-100}{2}=50\)[Ω]
\(R_{ab}=R_1+R=100+50=150\)[Ω]
H31.01-1A5
3 120[Ω]


\(R=\frac{\sqrt{横^2+4縦横} -横}{2}=\frac{\sqrt{R_1^2+4R_2R_1}-R_1}{2}\)
\(=\frac{\sqrt{100^2+4×24×100}-100}{2}=\frac{\sqrt{19600}-100}{2}=\frac{140-100}{2}=20\)[Ω]
\(R_{ab}=R_1+R=100+20=120\)[Ω]
検索用キーワード(問題文の最初の一文)
\(R_1\)と\(R_2\)の抵抗が無限に接続されている回路において、端子ab間から見た合成抵抗Rabの値
\(R_1\)[Ω]と\(R_2\)[Ω]の抵抗が無限に接続されている回路において、端子abから見た合成抵抗\(R_{ab}\)の値


コメント