R3.07-1A19
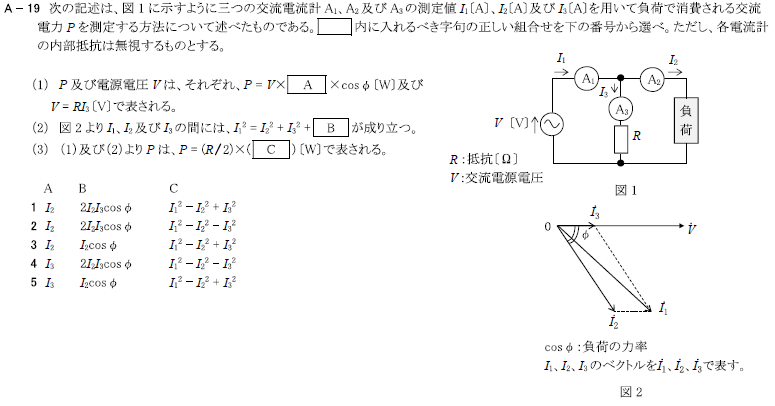
R2.01-1A20
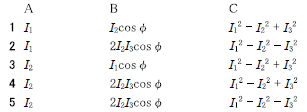
解答
R3.07-1A19
\(２ I_2 2I_2I_3\cos{φ} I^2_1-I_2^2-I_3^2\)
ワンポイント解説
三つの交流で にゃん（２）にゃん（２）言われて ひくひく（ー ー）する。
R2.01-1A20
\(５ I_2 2I_2I_3\cos{φ} I^2_1-I_2^2-I_3^2\)
ワンポイント解説
(1) \(R\)と負荷は並列接続なので、かかる電圧はともに\(V\)
負荷の電力\(P\)は電圧×電流より
\(P=V×I_2×\cos{φ}\)[W] ※電流は\(V\)と同じ向きになります。（皮相電力）
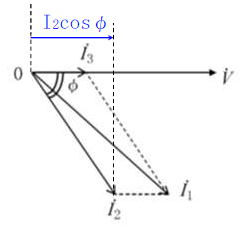
(2) 図２より\(I_1\)、\(I_2\)及び\(I_3\)の間には、\(I_1^2=I_2^2+I_3^2+（ Ｂ ）\)が成り立つ。
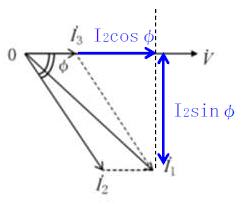
上図より、
\(I_1^2=(I_3+I_2\cos{φ})^2+(I_2\sin{φ})^2\)
\( =I_3^2+2I_2I_3\cos{φ}+I_2^2\cos{φ}^2+I_2^2\sin{φ}^2\)
\( =I_3^2+I_2^2(\cos{φ}^2+\sin{φ}^2)+2I_2I_3\cos{φ}\)
\( =I_2^2+I_3^2+2I_2I_3\cos{φ}\)
(3) (1)及び(2)より\(P\)は、\(P=(R/2)×（ Ｃ ）\)[W]で表される。
(1)より、\(P=V×I_2×\cos{φ}\)[W]
(2)より、\(\cos{φ}=\frac{I_1^2-I_2^2-I_3^2}{2I_2I_3}\)
\(P=VI_2\cos{φ}=RI_3I_2\cos{φ}=\frac{R}{2}×(I_1^2-I_2^2-I_3^2)\)[W]
検索用キーワード
３電流計の電力測定 図１に示すように三つの交流電流計 負荷で消費される交流電力Ｐを測定する方法について
コメント