R5.07-1A19

解答
R5.07-1A19
\(2 1-jωCR \sqrt{1+(ωCR)^2} \frac{1}{ωR}\sqrt{\frac{V_C^2}{V^2}-1}\)
ワンポイント解説
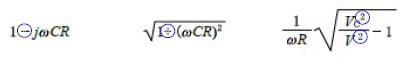
マイナス プラスの 事情(二乗)

(1)回路全体の合成インピーダンスが\(\dot{Z}_0\)
\(R\)と\(C\)の合成抵抗\(Z_C\)は、
\(Z_C=\frac{1}{\frac{1}{R}+jωC}=\frac{R}{1+jωCR}\)
\(L\)と\(Z_C\)は直列なので\(\dot{V}_C\)は
\(\dot{V}_C=\dot{V}×\frac{\dot{Z}_C}{\dot{Z}_0}\)
よって、
\(\frac{\dot{V}_C}{\dot{V}}=\frac{\dot{Z}_C}{\dot{Z}_0}=\frac{\frac{R}{1+jωCR}}{\frac{R}{1+ω^2C^2R^2}}=\frac{1+ω^2C^2R^2}{1+jωCR} ★=\frac{(1+jωCR)(1-jωCR)}{1+jωCR} ★=1-jωCR\)
★から★の展開が難しいですね。ポイントですので覚えてしまいましょう。
(2)\(\left| \frac{\dot{V}_C}{\dot{V}} \right|\)は(1)の大きさだから
\(\left| \frac{\dot{V}_C}{\dot{V}} \right|\)=\(\sqrt{1+(ωCR)^2}\)
(3)(2)より、両辺を二乗して
\((\frac{\dot{V}_C}{\dot{V}})^2=1+(ωCR)^2\)
\((ωCR)^2=(\frac{\dot{V}_C}{\dot{V}})^2-1\)
\(\sqrt{(ωCR)^2}=\sqrt{(\frac{\dot{V}_C}{\dot{V}})^2-1}\)
したがって、
\(C=\frac{1}{ωR}\sqrt{(\frac{\dot{V}_C}{\dot{V}})^2-1}\)
検索用キーワード(問題文の最初の一文)
図に示す回路を用いて静電容量C[F]を求める過程


コメント