R5.01-1A2
R4.01-1A3
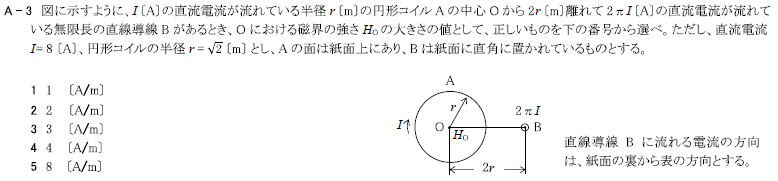
R2.11-1A3
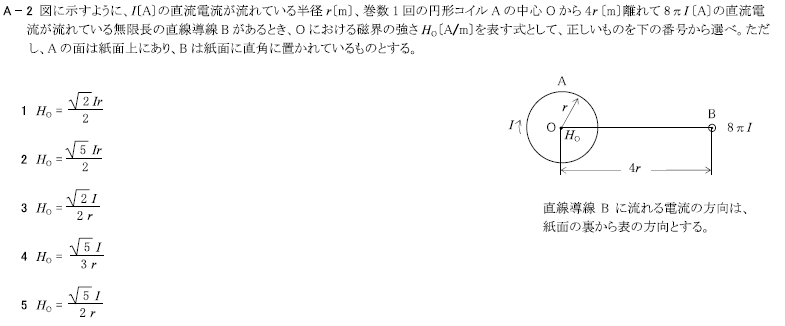
H31.01-1A2
解答
R5.01-1A2
\(２ H_o=\frac{\sqrt{10}I}{6r}\) ［A/m］
ワンポイント解説
①コイルＡ磁界の強さを求める
②直線導線Ｂ磁界の強さを求める
③コイルＡと直線導線Ｂの磁界の強さをベクトル和で求める。
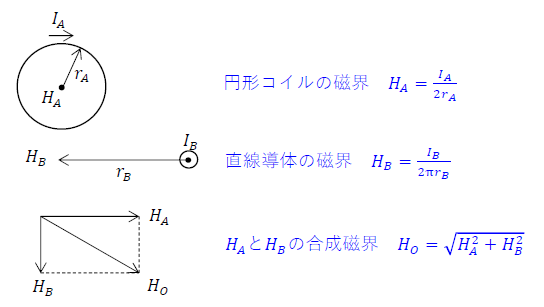
①コイルＡ磁界の強さを求める
\(H_A=\frac{I_A}{2r_A}=\frac{I}{2r}\)
②直線導線Ｂ磁界の強さを求める
\(H_B=\frac{I_B}{2πr_B}=\frac{πI}{2π×3r}=\frac{I}{6r}\)
③コイルＡと直線導線Ｂの磁界の強さをベクトル和で求める。
\(H_O=\sqrt{H_A^2+H_B^2}=\sqrt{(\frac{I}{2r})^2+(\frac{I}{6r})^2}=\sqrt{\frac{I^2}{4r^2}+\frac{I^2}{36r^2}}=\sqrt{\frac{9I^2+I^2}{36r^2}}=\frac{\sqrt{10}I}{6r}\)
R4.01-1A3
４ 4［A/m］
①コイルＡ磁界の強さを求める
\(H_A=\frac{I_A}{2r_A}=\frac{I}{2r}\)
②直線導線Ｂ磁界の強さを求める
\(H_B=\frac{I_B}{2πr_B}=\frac{2πI}{2π×2r}=\frac{I}{2r}\)
③コイルＡと直線導線Ｂの磁界の強さをベクトル和で求める。
\(H_O=\sqrt{H_A^2+H_B^2}=\sqrt{(\frac{I}{2r})^2+(\frac{I}{2r})^2}=\sqrt{\frac{I^2}{4r^2}+\frac{I^2}{4r^2}}=\sqrt{\frac{2I^2}{4r^2}}=\frac{\sqrt{2}I}{2r}\)
\(=\frac{\sqrt{2}×8}{2×\sqrt{2}}=4\)[A/m]
R2.11-1A3
\(３ H_o=\frac{I}{\sqrt{2}r}\)
①コイルＡ磁界の強さを求める
\(H_A=\frac{I_A}{2r_A}=\frac{I}{2r}\)
②直線導線Ｂ磁界の強さを求める
\(H_B=\frac{I_B}{2πr_B}=\frac{4πI}{2π×4r}=\frac{I}{2r}\)
③コイルＡと直線導線Ｂの磁界の強さをベクトル和で求める。
\(H_O=\sqrt{H_A^2+H_B^2}=\sqrt{(\frac{I}{2r})^2+(\frac{I}{2r})^2}=\sqrt{\frac{I^2}{4r^2}+\frac{I^2}{4r^2}}=\sqrt{\frac{2I^2}{4r^2}}=\frac{\sqrt{2}I}{2r}\)
\(=\frac{\sqrt{2}I\sqrt{2}}{2r\sqrt{2}}=\frac{I}{\sqrt{2}r}\)
H31.01-1A2
\(５ H_o=\frac{\sqrt{5}I}{2r}\)
①コイルＡ磁界の強さを求める
\(H_A=\frac{I_A}{2r_A}=\frac{I}{2r}\)
②直線導線Ｂ磁界の強さを求める
\(H_B=\frac{I_B}{2πr_B}=\frac{8πI}{2π×4r}=\frac{I}{r}\)
③コイルＡと直線導線Ｂの磁界の強さをベクトル和で求める。
\(H_O=\sqrt{H_A^2+H_B^2}=\sqrt{(\frac{I}{2r})^2+(\frac{I}{r})^2}=\sqrt{\frac{I^2}{4r^2}+\frac{I^2}{r^2}}=\sqrt{\frac{5I^2}{4r^2}}=\frac{\sqrt{5}I}{2r}\)
検索用キーワード
コイル・直線導体 直流電流が流れている半径 円形コイル 無限長の直線導体 磁界の強さ 紙面上にあり 紙面に直角に置かれているものとする
コメント