R5.07-2A18

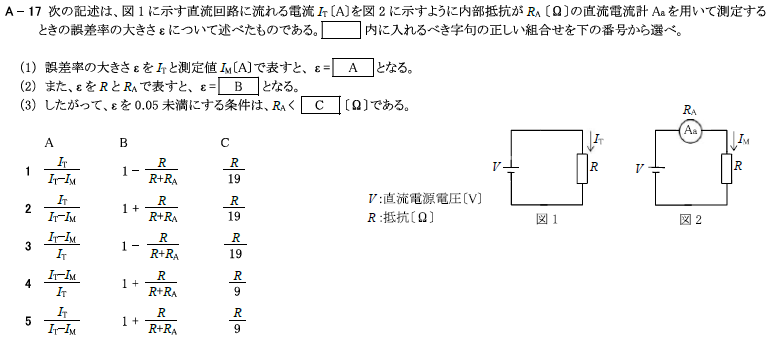
R5.01-1A17
R6.01-1A18
R4.01-2A18
R7.01-1A18

R4.01-1A18

解答
R5.07-2A18
\(2 \frac{I_M-I_T}{I_T} \frac{R}{R+R_A} \frac{R}{9}\)

・百分率誤差\(ε\)は以下の公式です。
\(ε=\frac{測定値-真値}{真値}×100=(\frac{測定値}{真値}-1)×100\) [%]
(3) \(ε\)を\(I_T\)と\(I_M\)で表すと、
\(ε=\frac{測定値-真値}{真値}=\frac{I_M-I_T}{I_T}\)となる。 -A
(4) また、\(ε\)を\(R\)と\(R_A\)で表すと、
\(ε=\frac{I_M-I_T}{I_T}=\frac{\frac{V}{R+R_A}-\frac{V}{R}}{\frac{V}{R}}\)
分母分子に\(\frac{R}{V}\)をかけて
\(=\frac{\frac{V}{R+R_A}×\frac{R}{V}-\frac{V}{R}×\frac{R}{V}}{\frac{V}{R}×\frac{R}{V}}=\frac{\frac{R}{R+R_A}-1}{1}=\frac{R}{R+R_A}-1\) -B
※誤差率は絶対値なのでBの答えは、分数-1でも1-分数のどちらでもOKです。
ただし、次に差し支えますので、次の問題は設問のとおりに進めます。
\(ε=1-\frac{R}{R+R_A}\)
ワンポイント解説
誤差率 ε=10[%]\(=\frac{R}{9}\) 5[%]\(=\frac{R}{19}\) 2[%]\(=\frac{R}{49}\)
(5) したがって、\(ε\)を0.1未満にする条件は、
Bの式が0.1未満になればよいので
\(ε=1-\frac{R}{R+R_A}<0.1\)
\(-\frac{R}{R+R_A}<-0.9\)
\(-R<-0.9R-0.9R_A\)
\(0.9R_A<0.1R\)
\(R_A<\frac{R}{9}\) -C
R5.01-1A17
3

・百分率誤差\(ε\)は以下の公式です。
\(ε=\frac{測定値-真値}{真値}×100=(\frac{測定値}{真値}-1)×100\) [%]
(1) \(ε\)を\(I_T\)と\(I_M\)で表すと、
\(ε=\frac{測定値-真値}{真値}=\frac{I_M-I_T}{I_T}\)、、、
答えが合わない時は、\(ε=\frac{真値-測定値}{真値}\)として、
\(ε=\frac{真値-測定値}{真値}=\frac{I_T-I_M}{I_T}\)となる。 -A
(2) また、\(ε\)を\(R\)と\(R_A\)で表すと、Aの式より、
\(ε=\frac{I_T-I_M}{I_T}=1-\frac{I_M}{I_T}\)
\(I_T=\frac{V}{R}\)
\(I_M=\frac{V×\frac{R}{R_A+R}}{R}=\frac{V}{R_A+R}\)
よって、\(ε\)に代入すると、
\(ε=1-\frac{I_M}{I_T}=1-\frac{V}{R_A+R}×\frac{R}{V}=1-\frac{R}{R_A+R}\) -B
ワンポイント解説
誤差率 ε=10[%]\(=\frac{R}{9}\) 5[%]\(=\frac{R}{19}\) 2[%]\(=\frac{R}{49}\)
(3) したがって、\(ε\)を0.05未満にする条件は、
Bの式が0.05未満になればよいので
\(ε=1-\frac{R}{R+R_A}<0.05\)
\(-\frac{R}{R+R_A}<-0.95\)
\(-R<-0.95R-0.95R_A\)
\(0.95R_A<0.05R\)
\(R_A<\frac{R}{19}\) -C
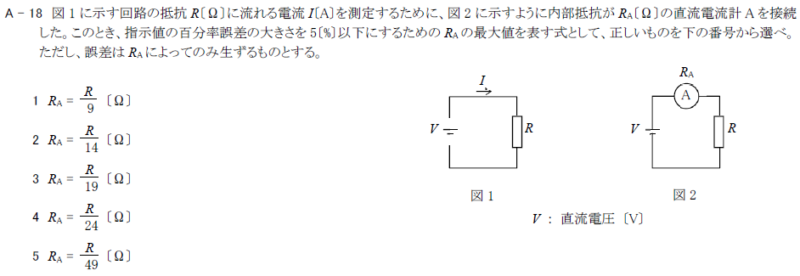
R6.01-1A18
\(3 R_A=\frac{R}{19}\)[Ω]

ワンポイント解説
誤差率 ε=10[%]\(=\frac{R}{9}\) 5[%]\(=\frac{R}{19}\) 2[%]\(=\frac{R}{49}\)
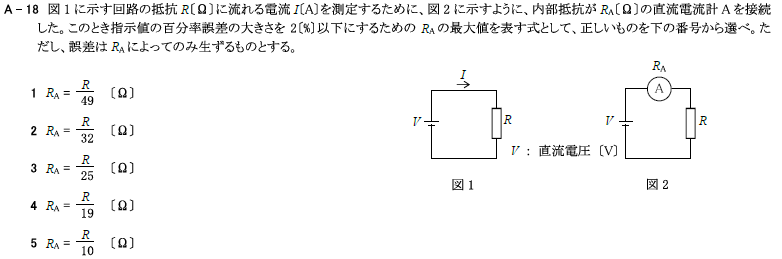
R4.01-2A18
\(1 R_A=\frac{R}{49}\)[Ω]

ワンポイント解説
誤差率 ε=10[%]\(=\frac{R}{9}\) 5[%]\(=\frac{R}{19}\) 2[%]\(=\frac{R}{49}\)
R7.01-1A18
2 電流計\(A_a\)の測定値\(I_M\)は、\(I_M=V/(R-R_A)\)誤 \(I_M=V/(R+R_A)\)正[A]である。

R4.01-1A18 ✕選択
5 εを0.1未満にする条件は、\(R_A>(R/9)\)誤 \(R_A<(R/9)\)正[Ω]である。
ワンポイント解説
誤差率 ε=10[%]\(=\frac{R}{9}\) 5[%]\(=\frac{R}{19}\) 2[%]\(=\frac{R}{49}\)

検索用キーワード(問題文の最初の一文)
図に示す直流電流計\(A_a\)を用いた回路において、電流を測定したときの誤差率の大きさ\(ε\)
図1に示す直流回路に流れる電流\(I_Γ\)[A]を図2に示すように内部抵抗が\(R_A\)[Ω]の直流電流計\(A_a\)を用いて測定するときの誤差率の大きさ\(ε\)
図1に示す回路の抵抗\(R\)[Ω]に流れる電流\(I\)[A]を測定するために、図2に示すように、内部抵抗が\(R_A\)[Ω]の直流電流計\(A\)を接続した。このときの指示値の百分率誤差の大きさを2[%]以下にするための\(R_A\)の最大値を表す式
図に示す直流電流計Aaを用いた回路において、電流を測定したときの誤差率の大きさε


コメント