AR8.01出題予想
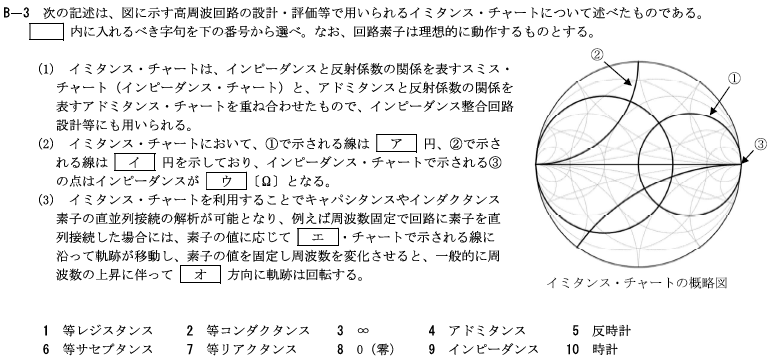
R5.07-2B3
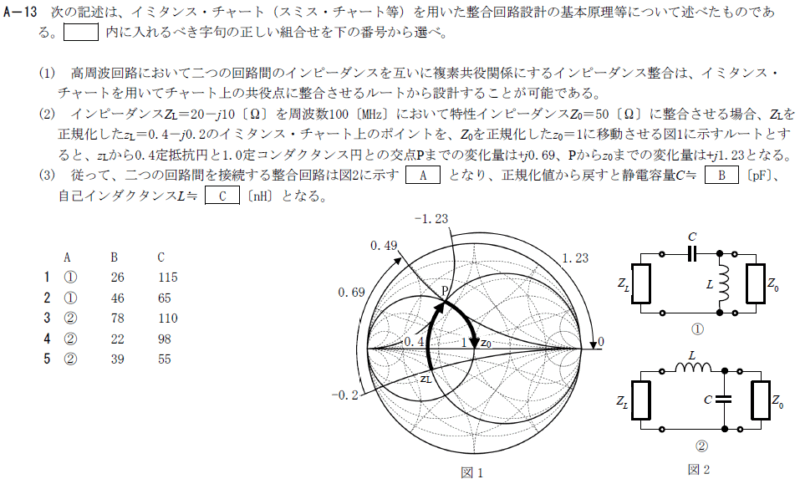
R7.01-1A13
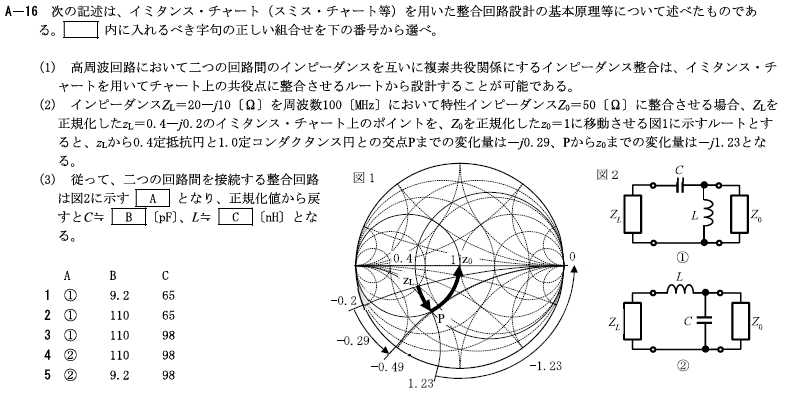
R5.01-2A16
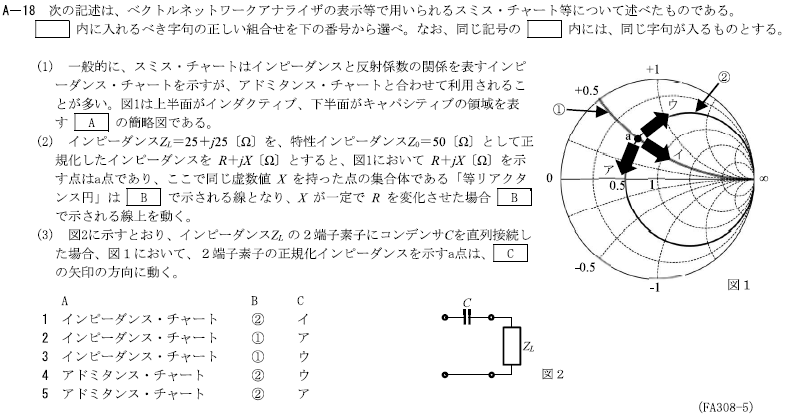
R3.07-2A18
解答
R5.07-2B3
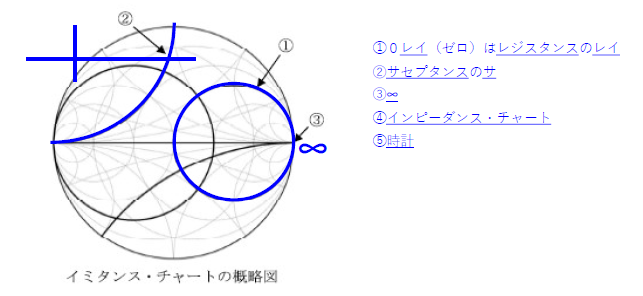
1 等レジスタンス
6 等サセプタンス
3 ∞
9 インピーダンス
10 時計
ワンポイント解説

R7.01-1A13
5 ② 39 55
ワンポイント解説
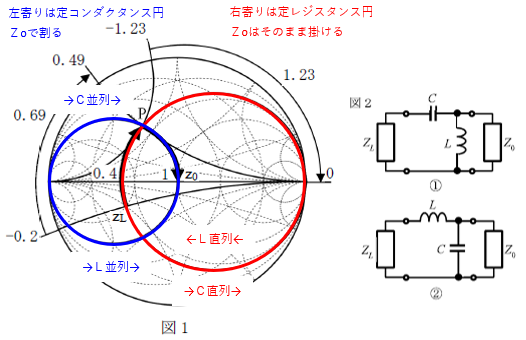

・\(z_L→P\)では、\(+j0.69Z_O=jωL\)より、
\(L=\frac{0.69Z_O}{ω}\)
\(=\frac{0.69×50}{2π×100M}\)
\(=\frac{0.69×50×10^{-8}}{2×3.14}\)
\(≒5.5×10^{-8}[H]\)
\(=55×10^{-9}[H]=55[nH]\)
・\(P→Z_O\)では、\(\frac{+j1.23}{Z_O}=\frac{1}{\frac{1}{jωC}}=jωC\)より、
\(\frac{1.23}{Z_O}=ωC\)
\(C=\frac{1.23}{ωZ_O}\)
\(=\frac{1.23}{2πfZ_O}\)
\(=\frac{1.23}{2π×100M×50}\)
\(=\frac{1.23}{π}×\frac{1}{10^{10}}\)
\(=0.39×10^{-10}\)
\(=0.01×39×10^{-10}\)
\(=39×10^{-12}[F]=39[pF]\)
R5.01-2A16
2 ① 110 65
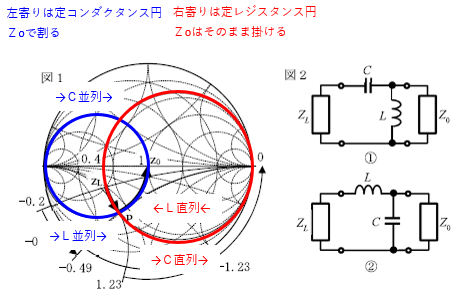

・\(z_L→P\)では、\(-j0.29Z_O=\frac{1}{jωC}=-j\frac{1}{ωC}\)より、
\(C=\frac{1}{0.29Z_Oω}\)
\(=\frac{1}{0.29×50×2π×100M}\)
\(=\frac{10^{-10}}{0.29×3.14}\)
\(=\frac{10^{-6}}{29×314}\)
ややこしい計算ですね。答えは[pF]なので\(p=10^{-12}\)を作っておきます。
\(=\frac{10^{6}×10^{-6}×10^{-6}}{29×314}\)
\(=\frac{10^{6}}{9106}p\)
\(=109.8≒110\)[pF]
・\(P→Z_O\)では、\(\frac{-j1.23}{Z_O}=\frac{1}{jωL}=-j\frac{1}{ωL}\)より、
\(L=\frac{Z_O}{1.23ω}\)
\(=\frac{50}{1.23×2π×100M}\)
\(=\frac{50×10^{-8}}{2.46×3.14}\)
\(=\frac{50×10^{-4}}{246×314}\)
ややこしい計算ですね。答えは[nH]なので\(n=10^{-9}\)を作っておきます。
\(=\frac{50×10^{5}×10^{-5}×10^{-4}}{246×314}\)
\(=\frac{50×10^{5}}{77,244}n\)
\(=64.7n≒65\)[nH]
R3.07-2A18
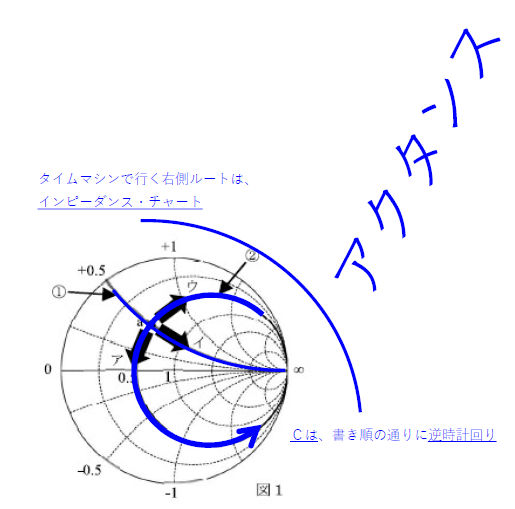
2 インピーダンス・チャート ① ア
ワンポイント解説

検索用キーワード(問題文の最初の一文)
・図に示す高周波回路の設計・評価等で用いられるイミタンス・チャート
・イミタンス・チャート(スミス・チャート等)を用いた整合回路設計の基本原理等
・ベクトルネットワークアナライザの表示等で用いられるスミス・チャート等


コメント