無線工学A1302

R6.01-1A15

R4.01-2A15

R5.07-2A14

解答

R6.01-1A15

４　0　　-2　　0

ワンポイント解説

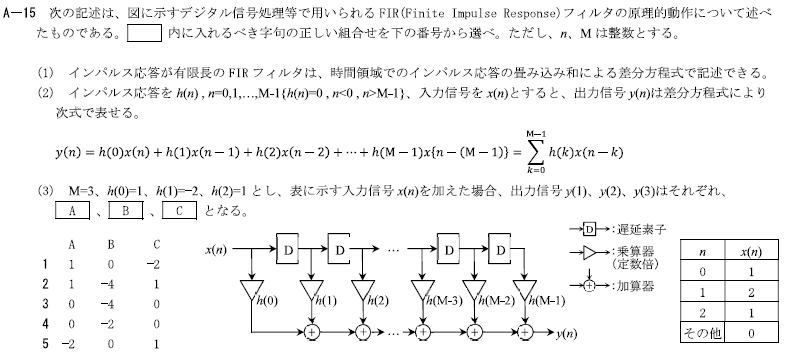
M=3の時、(2)の式は、
\(y(n)=\sum\limits_{k=0}^{M-1} h(k)x(n-k)=\sum\limits_{k=0}^{2} h(k)x(n-k)\)
　　\(=h(0)x(n)+h(1)x(n-1)+h(2)x(n-2)\)　－①
　↑\(=kが0の時+kが1の時+kが2の時\)の事です。

続いて、①式に\(h(0)=1、h(1)=-2、h(2)=1\)を表の\(n=1～3\)についてそれぞれ計算する。
\(n=1\)の時、\(y(1)=h(0)x(1)+h(1)x(0)+h(2)x(-1)\)
　　　　　　　　　\(=1×2+(-2)×1+1×0=0\)
\(n=2\)の時、\(y(2)=h(0)x(2)+h(1)x(1)+h(2)x(0)\)
　　　　　　　　　\(=1×1+(-2)×2+1×1=-2\)
\(n=3\)の時、\(y(3)=h(0)x(3)+h(1)x(2)+h(2)x(1)\)
　　　　　　　　　\(=1×0+(-2)×1+1×2=0\)

ちょっと分かりづらいと思いますので、丁寧に計算します。
①の式は、\(y(n)=h(0)x(n)+h(1)x(n-1)+h(2)x(n-2)\)
\(n=1\)の時、\(y(1)=h(0)x(1)+h(1)x(1-1)+h(2)x(1-2)\)
　　　　　　　　\(=h(0)x(1)+h(1)x(0)+h(2)x(-1)\)
　　　　　　　　\(x(n)\)は下の表から求めます
　　　　　　　　\(=1×2+(-2)×1+1×0=0\)

R4.01-2A15

５　4　　7　　6

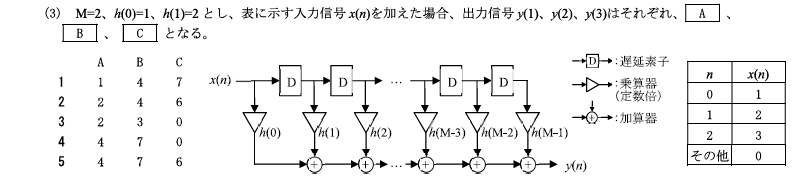
M=2の時、(2)の式は、
\(y(n)=\sum\limits_{k=0}^{M-1} h(k)x(n-k)=\sum\limits_{k=0}^{1} h(k)x(n-k)\)
　　\(=h(0)x(n)+h(1)x(n-1)\)　－①
続いて、①式に\(h(0)=1、h(1)=2\)を表の\(n=1～3\)についてそれぞれ計算する。
\(n=1\)の時、\(y(1)=h(0)x(1)+h(1)x(0)=1×2+2×1=4\)
\(n=2\)の時、\(y(2)=h(0)x(2)+h(1)x(1)=1×3+2×2=7\)
\(n=3\)の時、\(y(3)=h(0)x(3)+h(1)x(2)=1×0+2×3=6\)

R5.07-2A14

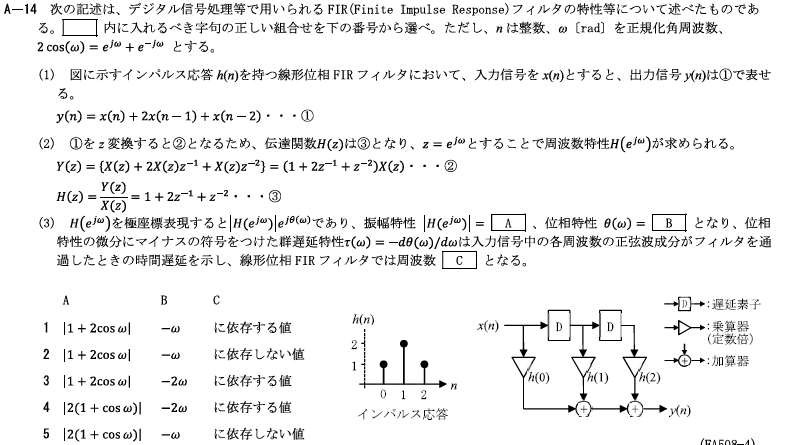
５　\(｜2(1+\cos{ω})｜　　-ω\)　　に依存しない値

ワンポイント解説
　\(｜2(1+\cos{ω})｜　　-ω\)　　に依存しない値
　ファイアー（FIR）コーヒー缶2本（2(　)）　マイナス1本（－ω）で　依存しない

検索用キーワード（問題文の最初の一文）

・図に示すデジタル信号処理等で用いられるFIR(Finite Impulse Response)フィルタの原理的動作
・デジタル信号処理等で用いられるFIR(Finite Impulse Response)フィルタの特性等