R5.07-2A17
R5.01-1A18
R4.01-1A17
R3.01-2A17
R1.07-1A17
解答
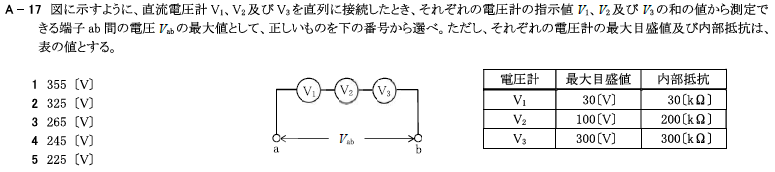
R5.07-2A17
３ 265［V］
ワンポイント解説
① それぞれの電圧計の最大電流を求める。
② ①の最小の電流しか、端子ab間には流せない。
（それ以上だと電圧計が壊れます。）
③ 端子ab間のオームの法則で電圧を求める。
① それぞれの電圧計の最大電流を求める。
\(I_1=\frac{最大メモリ値[V]}{内部抵抗[Ω]}\)
\(I_1=\frac{30}{30k}=1m[A]\)
\(I_2=\frac{100}{200k}=0.5m[A]\)
\(I_3=\frac{300}{300k}=1m[A]\)
② ①の最小の電流しか、端子ab間には流せない。
最小の電流は、\(I_2=0.5m[A]\)
③ 端子ab間のオームの法則で電圧を求める。
端子ab間の抵抗値Rは、
\(R=R_1+R_2+R_3=30k+200k+300k=530k[Ω]\)より、
求める電圧Vは、
\(V=R×I=530k×0.5m=265[Ω]\)
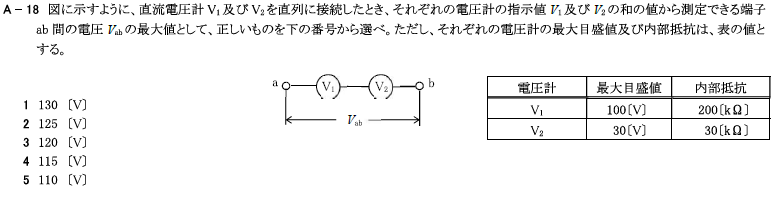
R5.01-1A18
４ 115［V］
① それぞれの電圧計の最大電流を求める。
\(I_1=\frac{最大メモリ値[V]}{内部抵抗[Ω]}\)
\(I_1=\frac{100}{200k}=0.5m[A]\)
\(I_2=\frac{30}{30k}=1m[A]\)
② ①の最小の電流しか、端子ab間には流せない。
最小の電流は、\(I_1=0.5m[A]\)
③ 端子ab間のオームの法則で電圧を求める。
端子ab間の抵抗値Rは、
\(R=R_1+R_2=200k+30k=230k[Ω]\)より、
求める電圧Vは、
\(V=R×I=230k×0.5m=115[Ω]\)
R4.01-1A17
４ 375［V］
① それぞれの電圧計の最大電流を求める。
\(I_1=\frac{最大メモリ値[V]}{内部抵抗[Ω]}\)
\(I_1=\frac{50}{50k}=1m[A]\)
\(I_2=\frac{100}{200k}=0.5m[A]\)
\(I_3=\frac{300}{500k}=0.6m[A]\)
② ①の最小の電流しか、端子ab間には流せない。
最小の電流は、\(I_2=0.5m[A]\)
③ 端子ab間のオームの法則で電圧を求める。
端子ab間の抵抗値Rは、
\(R=R_1+R_2+R_3=50k+200k+500k=750k[Ω]\)より、
求める電圧Vは、
\(V=R×I=750k×0.5m=375[Ω]\)
R3.01-2A17
２ 165［V］
① それぞれの電圧計の最大電流を求める。
\(I_1=\frac{最大メモリ値[V]}{内部抵抗[Ω]}\)
\(I_1=\frac{30}{30k}=1m[A]\)
\(I_2=\frac{150}{300k}=0.5m[A]\)
② ①の最小の電流しか、端子ab間には流せない。
最小の電流は、\(I_2=0.5m[A]\)
③ 端子ab間のオームの法則で電圧を求める。
端子ab間の抵抗値Rは、
\(R=R_1+R_2=30k+300k=330k[Ω]\)より、
求める電圧Vは、
\(V=R×I=330k×0.5m=165[Ω]\)
R1.07-1A17
３ 318［V］
① それぞれの電圧計の最大電流を求める。
\(I_1=\frac{最大メモリ値[V]}{内部抵抗[Ω]}\)
\(I_1=\frac{30}{30k}=1m[A]\)
\(I_2=\frac{300}{500k}=0.6m[A]\)
② ①の最小の電流しか、端子ab間には流せない。
最小の電流は、\(I_2=0.6m[A]\)
③ 端子ab間のオームの法則で電圧を求める。
端子ab間の抵抗値Rは、
\(R=R_1+R_2=30k+500k=530k[Ω]\)より、
求める電圧Vは、
\(V=R×I=530k×0.6m=318[Ω]\)
検索用キーワード
電圧計の直列接続 直流電圧計\(V_1\)、\(V_2\)及び\(V_3\)を直列に接続したとき、それぞれの電圧計の指示値\(V_1\)、\(V_2\)及び\(V_3\)の和の値から測定できる端子ab間の電圧\(V_{ab}\)の最大値として、正しいものを下の番号から選べ。ただし、それぞれの電圧計の最大目盛値及び内部抵抗は、表の値とする。
直流電圧計\(V_1\)及び\(V_2\)を直列に接続したとき、それぞれの電圧計の指示値\(V_1\)及び\(V_2\)の和の値から
コメント