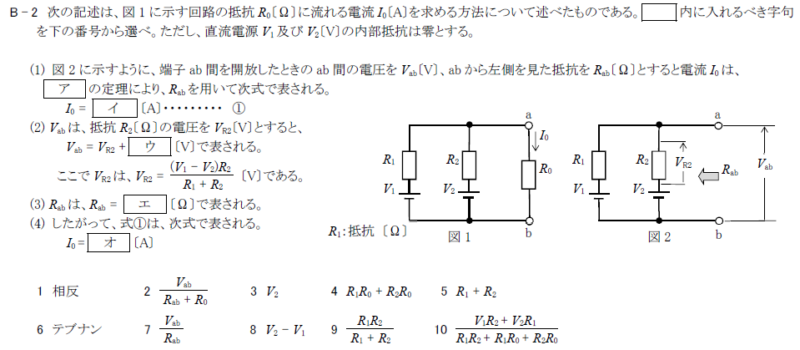
R6.01-1B2
R4.01-2B2
R2.01-1B2
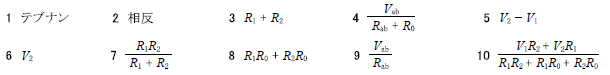
解答
R6.01-1B2
ア 6:テブナン
イ 2:\(\frac{V_{ab}}{R_{ab}+R_0}\)
ウ 3:\(V_2\)
エ 9:\(\frac{R_1R_2}{R_1+R_2}\)
オ 10:\(\frac{V_1R_2+V_2R_1}{R_1R_2+R_1R_0+R_2R_0}\)

ワンポイント解説
テブナンの定理 ※負荷\(R_0\)を開放したのがテブナンの定理
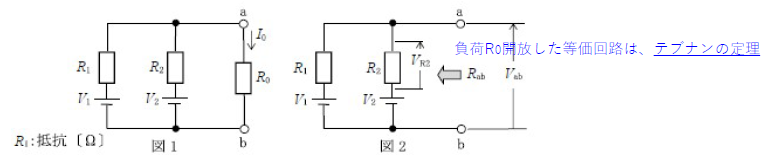
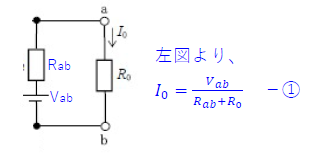
ワンポイント解説 (1)を図にすると
ワンポイント解説 (2)
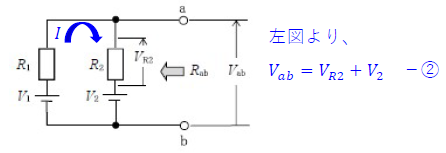
ワンポイント解説 (3)
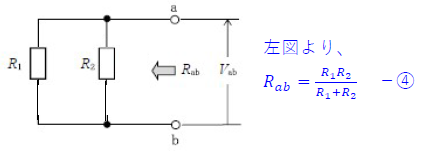
ワンポイント解説 (4)
式①は、\(I_0=\frac{V_{ab}}{R_{ab}+R_0}\)
\(I_0=\frac{V_{R2}+V_2}{\frac{R_1R_2}{R_1+R_2}+R_0}=\frac{\frac{V_1-V_2}{R_1+R_2}R_2+V_2}{\frac{R_1R_2}{R_1+R_2}+\frac{R_0(R_1+R_2)}{R_1+R_2}}=\frac{(V_1-V_2)R_2+V_2(R_1+R_2)}{R_1R_2+R_0(R_1+R_2)}\)
\(=\frac{V_1R_2-V_2R_2+V_2R_1+V_2R_2}{R_0R_1+R_1R_2+R_2R_0}=\frac{V_1R_2+V_2R_1}{R_1R_2+R_1R_0+R_2R_0}\)
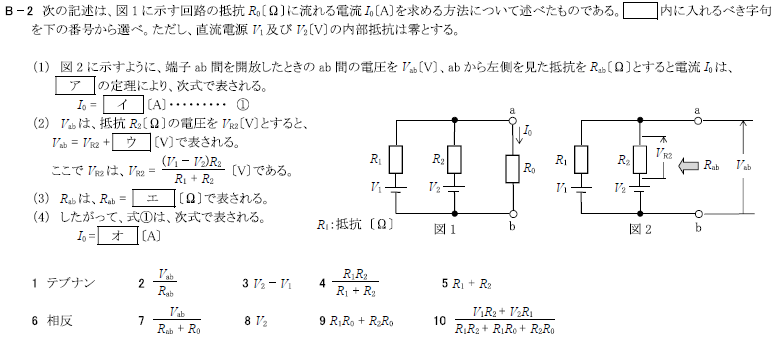
R4.01-2B2
ア 1:テブナン
イ 7:\(\frac{V_{ab}}{R_{ab}+R_0}\)
ウ 8:\(V_2\)
エ 4:\(\frac{R_1R_2}{R_1+R_2}\)
オ 10:\(\frac{V_1R_2+V_2R_1}{R_1R_2+R_1R_0+R_2R_0}\)

R2.01-1B2
ア 1:テブナン
イ 4:\(\frac{V_{ab}}{R_{ab}+R_0}\)
ウ 6:\(V_2\)
エ 7:\(\frac{R_1R_2}{R_1+R_2}\)
オ 10:\(\frac{V_1R_2+V_2R_1}{R_1R_2+R_1R_0+R_2R_0}\)
検索用キーワード(問題文の最初の一文)
図1に示す回路の抵抗\(R_0\)[Ω]に流れる電流\(I_0\)[A]を求める方法


コメント