基礎318

R3.01-2A13

解答

R3.01-2A13

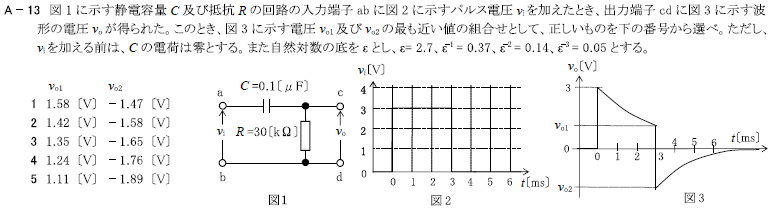
５　1.11［V］　　　-1.89［V］

ワンポイント解説
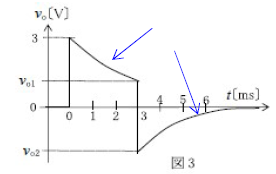
　この波形（青矢印）が出たら、
　①\(V_{o1}=V_o×ε^x\)
　　　　\(ε^x\)は、\(ε、ε^{-1}、ε^{-2}、ε^{-3}\)の中から選ぶ。
　②\(ε^x\)の選び方
　　\(x=\frac{t}{CR}\)
　③\(V_{o2}=V_{o1}-V_{o}\)

　①\(V_{o1}=V_o×ε^x\)
　　　　\(ε^x\)は、\(ε、ε^{-1}、ε^{-2}、ε^{-3}\)の中から選ぶ。
　②\(ε^x\)の選び方
　　\(x=\frac{t}{CR}=\frac{3m}{0.1μ×30k}=\frac{3}{3}=1\)
　　　※\(t\)は、\(V_{o1}\)の時間をグラフから読み取る。この場合、\(t=3[ms]\)
　①\(V_{o1}=V_o×ε^{-1}=3×0.37=1.11[V]\)
　③\(V_{o2}=V_{o1}-V_{o}=1.11-3=-1.89[V]\)

検索用キーワード

方形パルスのＣＲ出力　静電容量　抵抗　回路の入力端子　パルス電圧　Cの電荷は零とする。　自然対数の底をεとし