R7.01-1A4

R4.01-2A2

解答
R7.01-1A4
1 1 3
ワンポイント解説
■相互インダクタンス \(M=k\sqrt{L_1L_2}\)
\(k\):結合係数、\(L_1\):自己インダクタンス1、\(L_2\):自己インダクタンス2
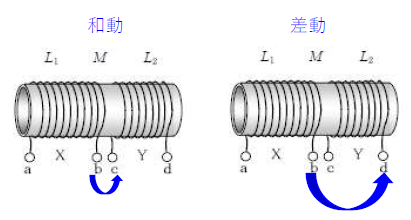
■和動接続 \(L_{ad}=L_1+L_2+2M\)
■差動接続 \(L_{ac}=L_1+L_2-2M\)

(1) 相互インダクタンス \(M=k\sqrt{L_1L_2}\)より、
\(M=k\sqrt{L_1L_2}=\frac{1}{2}\sqrt{4m×1m}=\frac{2m}{2}=1\)[mH]
(2) 端子bと端子dの接続は差動接続 \(L_{ac}=L_1+L_2-2M\)より、
\(L_{ac}=L_1+L_2-2M=4m+1m-2×1m=3\)[mH]
R4.01-2A2
\(2 和動 L_1+L_2+2M L_{ad}-L_{ac}\)

■和動接続 \(L_{ad}=L_1+L_2+2M\) ー①
■差動接続 \(L_{ac}=L_1+L_2-2M\) ー②
①-②は、
\(L_{ad}-L_{ac}=4M\)
\(M=\frac{L_{ad}-L_{ac}}{4}\)
検索用キーワード(問題文の最初の一文)
図に示す自己インダクタンスL1=4〔mH〕及びL2=1〔mH〕のコイルを直列に接続したときの合成インダクタンス
図に示すような円筒に、同一方向に巻かれた二つのコイルX及びYの合成インダクタンス及びXY間の相互インダクタンスの原理


コメント