R4.07-1A20
解答
R4.07-1A20
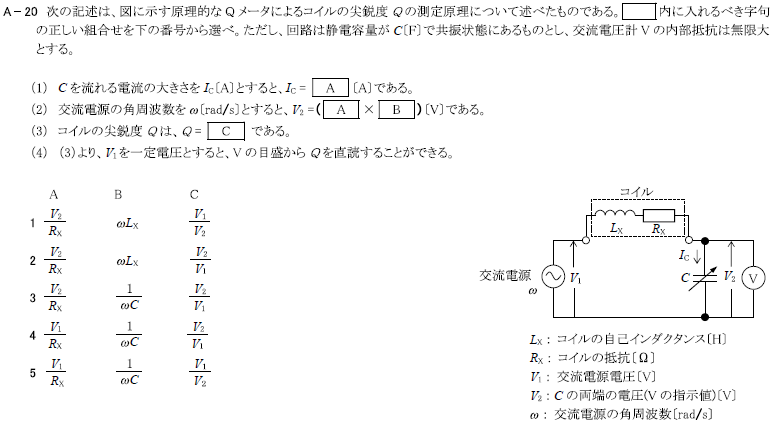
\(４ \frac{V_1}{R_X} \frac{1}{ωC} \frac{V_2}{V_1}\)
ワンポイント解説
解き方
①回路全体のインピーダンスＺを求める
②直列共振状態なので①の虚数部が０になる
③(1)～(3)を解く
①回路全体のインピーダンスを\(Z\)とすると、
\(Z=jωL_X+R_X+\frac{1}{jωC}=R_X+jωL_X-j\frac{1}{ωC}=R_X+j(ωL_X-\frac{1}{ωC})\)
②直列共振状態なので①の虚数部が０になる
\(Z=R_X+j(ωL_X-\frac{1}{ωC}) ( )内が0なので、\)
\(Z=R_X\)
③(1)～(3)を解く
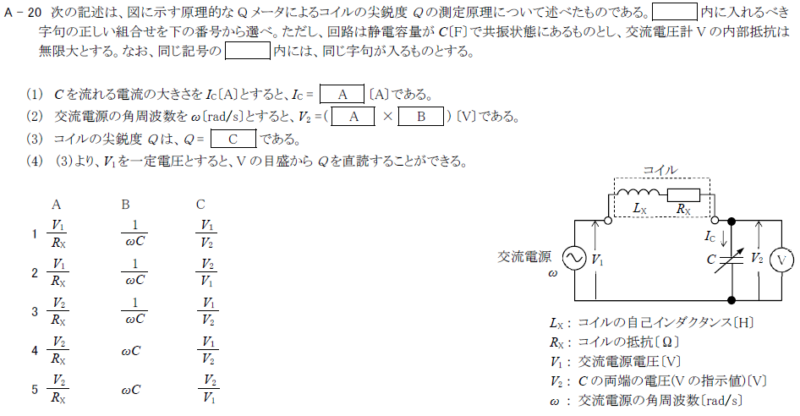
(1)\(C\)を流れる電流の大きさを\(I_C\)とすると、
\(I_C=\frac{V_1}{Z}=\frac{V_1}{R_X}\)
※\(V_2\)でないことに注意。
(2)コンデンサの電圧\(V_2\)は、オームの法則より
\(V_2=I_C×\frac{1}{ωC}\)
\(V_2=\frac{V_1}{R_X}×\frac{1}{ωC}\)
(3)コイルの先鋭度\(Q\)は
\(Q=\frac{ωL_X}{R_X}=\frac{1}{ωCR_X}\)
(2)の式
\(V_2=\frac{V_1}{R_X}×\frac{1}{ωC}\)より
\(\frac{1}{ωCR_X}=\frac{V_2}{V_1}\)
\(Q=\frac{1}{ωCR_X}=\frac{V_2}{V_1}\)
検索用キーワード
Qメーター 図に示す原理的なＱメータによるコイルの尖鋭度Ｑの測定原理について述べたものである。
コメント