基礎102

基礎令和7年1月出題予想

R5.07-1A2

R3.01-2A2

R1.07-1A2

R3.07-1A2

解答

R5.07-1A2

\(３　\frac{Q}{2πε_or}\)［V］

ワンポイント解説
　\(V_{cd}=2kQ(\frac{1}{R}-\frac{1}{D})　　　k=\frac{1}{4πε_o}\)
　\(R、D\)は下記図を参照。

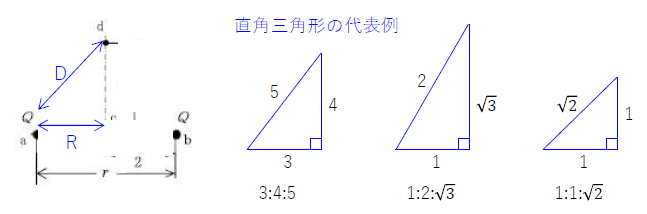
\(1:2:\sqrt{3}\)の直角三角形。
\(R=\frac{r}{2}、D=r、k=\frac{1}{4πε_o}\)となるので、
\(V_{cd}=2kQ(\frac{1}{R}-\frac{1}{D})=\frac{2Q}{4πε_o}(\frac{1}{\frac{r}{2}}-\frac{1}{r})=\frac{Q}{2πε_o}(\frac{2}{r}-\frac{1}{r})=\frac{Q}{2πε_or}\)［V］

R3.01-2A2

\(１　\frac{Q}{2πε_or}\)［V］

R1.07-1A2

\(２　\frac{Q}{3πε_or}\)［V］

比率が謎の直角三角形。
\(R=r、Dは三平方の定理より、D=\sqrt{r^2+(2\sqrt{2}r)^2}=\sqrt{9r^2}=3r、k=\frac{1}{4πε_o}\)となるので、
\(V_{cd}=2kQ(\frac{1}{R}-\frac{1}{D})=\frac{2Q}{4πε_o}(\frac{1}{r}-\frac{1}{3r})=\frac{Q}{2πε_o}×\frac{2}{3r}=\frac{Q}{3πε_or}\)［V］

R3.07-1A2

\(４　0.1kqQ［J］\)

\(3:4:5\)の直角三角形。
\(R=4、D=5、\frac{1}{4πε_o}=k\)となるので、
\(V_{cd}=2kQ(\frac{1}{R}-\frac{1}{D})=2kQ(\frac{1}{4}-\frac{1}{5})=2kQ×\frac{1}{20}=0.1kQ\)
仕事量W［J］は、cからoまでの電位差×点電荷qより、
\(W=V_{cd}×q=0.1kqQ\)［J］

検索用キーワード（問題文の最初の一文）

真空中でr[m]離れた点a及びbにそれぞれ点電荷Q[C]（Q>0）が置かれているとき、線分abの中点cと、cから線分abに垂直方向に\(\sqrt{3}r/2\)[m]離れた点dとの電位差の値
真空中で2r[m]離れた点a及びbにそれぞれ点電荷Q[C]（Q>0）が置かれているとき、線分abの中点cと、cから線分abに垂直方向に\(2\sqrt{2}r\)[m]離れた点dとの電位差の値
真空中で8[m]離れた点a及びbにそれぞれ点電荷Q[C]（Q>0）が置かれている。点a、b間の中点Oから線分abと垂直方向に3[m]離れた点cからOまで点電荷q[C](q>0)を移動させるのに必要な仕事量